Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas - Ex. 111

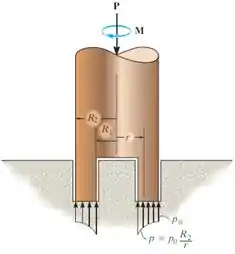
Assumindo que a variação de pressão no fundo do mancal axial seja definida como p = p o ( R 2 r ) , determine o torque M necessário para superar o atrito se o eixo está sujeito a uma força axial P . O coeficiente de atrito estático é μ s . Para a solução, é preciso determinar p o em termos de P e as dimensões do mancal R 1 e R 2 .

Passo 1

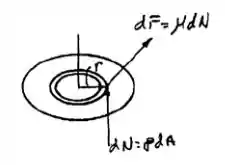
Vamos desenhar o diagrama de corpo livre dessa situação para entendermos a situação da nossa questão! Para a base do mancal, temos:

Passo 2

Essa questão é boa de fazer, vamo que vamo! Para um sistema em equilíbrio, o somatório das forças nos eixos de referência ( x , y , z ) e o somatório dos momentos em relação a um ponto são iguais a zero. Assim, para essa questão, vamos começar a analisar pelo somatório de forças no eixo z .

∑ F z = 0

- P + ∫ d N = 0

O elemento diferencial da força normal pode ser escrita como d N = p d A . Assim,

P = ∫ 0 2 π ∫ R 1 R 2 p r   d r   d θ

P = ∫ 0 2 π ∫ R 1 R 2 p o R 2 r r   d r   d θ

P = 2 π p o R 2 R 2 - R 1

p o = P 2 π R 2 ( R 2 - R 1 )

Passo 3

A força normal atuando no elemento diferencial de área d A é d N = p d A = p r d r d θ . Além disso, a força de atrito atuando nesse elemento diferencial é dada por d F = μ s d N = μ S p r d r d θ . A equação do momento sobre o eixo da embreagem é:

∑ M = 0

M - ∫ r d F = 0

M = ∫ 0 2 π ∫ R 1 R 2 μ s p r 2 d r   d θ

M = ∫ 0 2 π ∫ R 1 R 2 μ s p o R 2 r r 2 d r   d θ

M = μ s 2 π p o R 2 1 2 R 2 2 - R 1 2

Passo 4

No passo 2 encontramos o valor para p o , certo? Vamos usar essa expressão e substituí-la na equação do momento!

M = μ s 2 π P 2 π R 2 R 2 - R 1 R 2 1 2 R 2 2 - R 1 2

M = 1 2 μ s P R 2 - R 1 R 2 + R 1 R 2 - R 1

M = 1 2   μ s P ( R 2 + R 1 )  

Resposta

O torque M exigido para superar o atrito é igual a:

M = 1 2   μ s P ( R 2 + R 1 )  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco de embreagem é usado nas transmissões de automóveis padrão. Se quatro molas são usadas para manter os dois discos A e B juntas, determine a força em cada mola necessária para transmitir um mom
Se P = 900N for aplicado ao cabo da alavanca L , determine o torque máximo M que a embreagem pode transmitir. O coeficiente de atrito estático na superfície em contato é μ s = 0,3 .
O mancal axial está sujeito a uma distribuição de pressão parabólica em sua superfície de contato. Se o coeficiente de atrito estático é μ s , determine o torque M necessário para superar o atrito e g
Devido ao desgaste nas bordas, o mancal axial está sujeito a uma distribuição de pressã cônica em sua superfície de contato. Determine o torque M necessário para superar o atrito e girar o eixo, que s
Se a mola exerce uma força de 4500N sobre o bloco determine o torque M necessário para girar o eixo. O coeficiente de atrito estático em todas as superfícies de contato é μ s = 0,3 .