Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 196
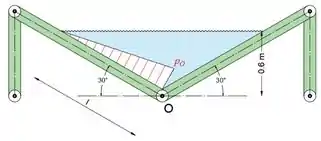
Os lados de uma calha de água doce em forma de V, mostrado na seção, são articuladas ao longo de sua interseção comum através de O e são apoiadas em cada lado por escoras verticais articuladas em cada extremidade e espaçadas a cada 2 m. Calcule a compressão C em cada biela. Negligencie os pesos dos membros.
Passo 1
E ai gurizada tudo belezinha???
Observe que para determinar a compactação C na rua, precisaremos calcular a pressão que atua na parede da água. Observe também que a água está sempre agindo normal à superfície, e a expressão para pressão na profundidade h é:
Como a densidade da água é: e a gravidade é , podemos escrever a expressão acima como:
No esboço abaixo, podemos ver que o ponto O está na profundidade de:
Portanto, a pressão atuando no ponto O é:
No esboço abaixo, podemos ver que o comprimento da superfície de contato entre a água e a parede é:
Passo 2
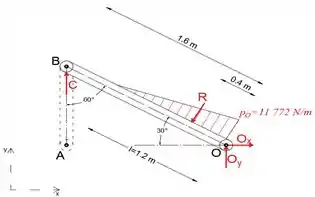
A seguir, isolaremos e desenharemos o diagrama de corpo livre da parede.
Observe que o trecho AB é um membro de duas forças, o que significa que a linha de ação da força de compressão C passa por ambas as articulações A e B.
Substituímos a carga distribuída por seu resultado e que atua no centro do triângulo.
Passo 3
Ao igualar a soma dos momentos sobre o ponto O a zero, eliminaremos as forças de reação em O, então a única incógnita será a força C.
A partir daqui, podemos expressar a força C como:
Substitua R, por seu valor.
Resposta
- Calculando a expressão acima, obtivemos que a força C na biela é: