Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 125

Um caminhão desce uma ladeira com 4% de inclinação a uma velocidade de 90 km/h, quando os freios são aplicados para desacelerá-lo até 30 km/h. Um sistema de freios antiderrapantes limita a força de frenagem a um valor no qual as rodas do caminhão ficam na iminência de deslizar. Sabendo que o coeficiente de atrito estático entre a estrada e as rodas é de 0,60, determine o menor tempo necessário para o caminhão reduzir a velocidade.

Passo 1

Para determinar o menor tempo necessário para o caminhão reduzir a velocidade, vamos utilizar o princípio de impulso e quantidade de movimento linear. Antes, vamos representar as forças por meio do diagrama de corpo livre. Para o caminhão em desaceleração descendo uma ladeira, temos o seguinte esquema:

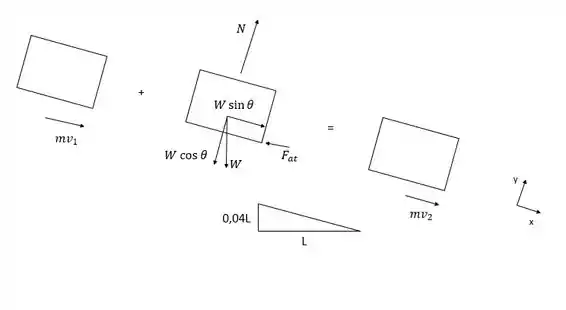
Onde v 1 = 90   k m / h , v 2 = 30   k m / h e N = W cos ⁡ θ .

Passo 2

A equação que relaciona o impulso e a quantidade de movimento linear pode ser expressa por:

m v → 1 + ∑ I m p → 1 → 2 = m v → 2

Como as velocidades estão em km/h, vamos converter para m/s:

v 1 = 90   ÷ 3,6 = 25   m / s

v 2 = 90 ÷ 3,6 = 8,33   m / s

Para obtermos θ , utilizaremos o triângulo retângulo abaixo do diagrama de corpo livre. A ladeira possui 4% de inclinação, ou seja, a altura da ladeira equivale a 4% do comprimento caso a desaceleração ocorresse em um plano sem inclinação. Assim, temos:

tan ⁡ θ = 0,04 L L → θ = arctan ⁡ 0,04 = 2,29 °

Para a direção x, o impulso é dado por:

I m p x = W sin ⁡ θ t - μ k N t = m g sin ⁡ θ t - m μ k g cos ⁡ θ t

Passo 3

Substituindo os termos do passo 2 na equação descrita no passo 1, temos:

m v 1 + m g sin ⁡ θ t - m μ k g cos ⁡ θ t = m v 2

t = v 1 - v 2 g ( μ k cos ⁡ θ - sin ⁡ θ ) = 25 - 8,33 9,81 ( 0,60 cos ⁡ 2,29 ° - sin ⁡ 2,29 ° ) = 3,04   s

Logo, o tempo mínimo para o caminhão reduzir a velocidade é t = 3,04 s

Resposta

t = 3,04 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada uma das duas barras uniformes A de 300m m possui uma massa de 1,5k g e é articulada em sua extremidade à base B que está girando. A base com 4k g tem um raio de giração de 40m m e está inicialmen
A roda de 30k g tem um raio de giração em relação a seu centro de 75m m e está girando no sentido horário na taxa de 300r p m , quando é liberada no plano inclinado sem velocidade em seu centro O . En
A caixa de 100 kg é içada pelo motor M . Se a velocidade da caixa aumenta uniformemente, de 1,5 m/s para 4,5 m/s em 5 segundos, determine a tração desenvolvida no cabo durante o movimento.
A balia jubarte de 5,5 Mg está encalhada na praia, devido à variação na maré. Em um esforço para resgatar a baleia, um barco rebocador de 12 Mg é utilizado para libertá-la empregando uma corda inexten
A caixa de 100 kg é içada pelo motor M . O motor excerce no cabo uma força T = 200 t 1 / 2 + 150N onde t está em segundos. Se a caixa parte do repouso no solo, determine a velocidade da caixa quando t