Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 233

A barra esbelta uniforme de 1,2   m com roletes leves na extremidade é liberada a partir do repouso no plano vertical com θ praticamente nulo. Determine e represente graficamente a velocidade de A como uma função de θ e encontre a velocidade máxima de A e o ângulo correspondente θ .

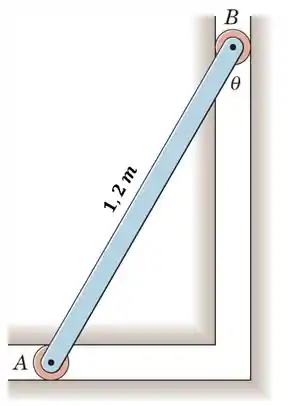
Passo 1

Primeiramente é necessário determinar o DC do corpo em análise, confomer a figura abaixo mostra.

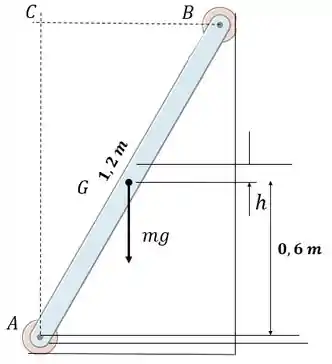
Passo 2

A velocidade de A pode se determinada apartir da relação de energia pontencial gravitacional e cinética.

∆ E C = ∆ E g

Sendo,

∆ E C = 1 2 I G ω 2  

I G = 1 3 m l 2

I G = 1 3 m ( 1,2 ) 2

∆ E C = 1 2 I c ω 2  

∆ E C = 1 2 1 3 m ( 1,2 ) 2 ω 2 = 0,24 m ω 2

E,

∆ E g = m g h

∆ E g = m g ( 0,6 - 0,6 cos ⁡ θ )

∆ E g = 0,6 m g ( 1 - cos ⁡ θ )

Então,

∆ E C = ∆ E g

0,24 m ω 2 = 0,6 m g ( 1 - cos ⁡ θ )

ω = ( 2,5 ( 9,81 ) ( 1 - cos ⁡ θ )   r a d / s

ω = 4,95227 ( 1 - cos ⁡ θ )   r a d / s

Passo 3

Utilizando a velocidade relativa entre as direções do movimento pode se determinar a velocidade de A

v A = v B + v A / B

v A = v A / B c o s ( θ ) = L ω c o s ⁡ ( θ )

v A =   1,2 ( 24,525 ( 1 - cos ⁡ θ )   c o s ⁡ ( θ )

v A = 5,94273 1 - cos ⁡ θ c o s ⁡ ( θ )

v m a x = 2,29   m / s     e m     θ = 48,19 °

Resposta

A expressão de v A em função de θ é v A = 5,94 1 - cos ⁡ θ c o s ⁡ ( θ ) . E o valor máximo de velocidade é v m a x = 2,29   m / s     e m     θ = 48,19 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro atinge um poste de luz, o qual é projetado para romper-se em sua base com resistência desprezível. De um vídeo feito da colisão, é observado que o poste foi submetido a uma velocidade angular
O satélite de 200 kg tem um raio de giração em relação ao eixo z centroidal é k z = 1,25m . Inicialmente, ele está girando com uma velocidade angular constante ω 0 = 1500 kr e v / m i n . Se os dois j
Se o eixo é submetido a um torque M = 15 t 2N . m , onde t é dado em segundos, determine a velocidade angular do conjunto quando t = 3 s, partindo do repouso. As barras AB e BC, cada uma, têm uma mass
Se o eixo é submetido a um torque M = 30 e - 0,1 tN . m , onde t é dado em segundos, determine a velocidade angular da montagem qundo t = 5 s, partindo do repouso. A placa retangular tem uma massa de
A estrutura do rolo tem uma massa de 5,5 Mg e um centro de massa em G. O rolo tem uma massa de 2 Mg e um raio de giração em relação a seu centro de massa k A = 0,45m . Se um torque M = 600 N.m é aplic