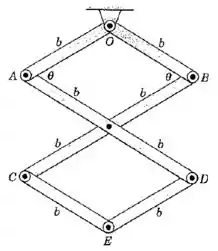
Cada uma das barras articuladas possui uma massa por unidade de comprimento, e o conjunto está suspenso em , no plano vertical. Se as barras são liberadas a partir do repouso com praticamente nulo, determine a velocidade angular comum a todas as barras quando , , e se juntam.

Quando o ângulo é praticamente nulo, podemos imaginar todo o sistema “empilhado” em uma única reta.

Nesse caso, os pontos e estarão um por cima do outro, e o mesmo vale para o par e o par , . Portanto o centro de massa do sistema estará na altura do ponto fixo .

Mais tarde, depois que o sistema já foi liberado e o ângulo é próximo de , os mesmos pares estarão sobrepostos novamente. Nesse caso, o centro de massa do sistema estarã na metade do comprimento dessa barra:

Se colocarmos o “zero” da nossa energia potencial na altura do ponto , podemos dizer que a variação da energia potencial do sistema foi:

E a massa pode ser calculada em função da densidade por unidade de comprimento:

Então: