Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 26
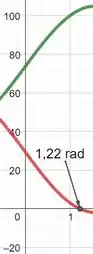
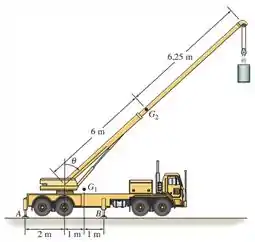
O caminhão é simetricamente apoiado no solo por duas extensões laterais em e duas em , descarregando sua suspensão e dando estabilidade contra o tombamento. Se o guindaste e o caminhão possuem massa de 18 Mg e centro de massa em , e a lança possui massa de 1,8 Mg e centro de massa em , determine as reações verticais em cada um dos quatro apoios no solo em função do ângulo de lança quando a lança estiver suportando uma carga de 1,2 Mg. Represente em gráfico os resultados medidos de até o ângulo crítico onde começa a ocorrer uma inclinação do veículo.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão bem tranquila. Não se assustem pelas massas estarem na ordem de e também pela questão pedir o gráfico de uma função!
Outro ponto aqui importante é lembrarmos que, aonde vemos um apoio em e um apoio em , na verdade, temos dois!!! Então, vamos sempre contabilizar duas forças neste local, certo?
Então, vamos as contas!
Passo 2
Para determinarmos as reações normais nos apoios, vamos ter que avaliar o equilíbrio dos momentos em relação aos pontos e através do somatório dos momentos.
Desta forma, vamos começar determinando a normal em . Para isto, fazemos o somatório em relação ao ponto . Logo,
Já para determinarmos a força normal em , vamos fazer o somatório em relação ao ponto . Logo,
E assim acabamos de determinar as reações nos apoios em e em !
Passo 3
Para finalizarmos a questão, temos que esboçar o gráfico das forças normais e até o momento em que o veículo começa a inclinar.
Mas quando isto ocorre? Isto ocorrerá a partir do momento em quem alguma dessas forças normais passa a ser negativo, o que não faz sentido algum! Sendo assim, temos o seguinte gráfico!
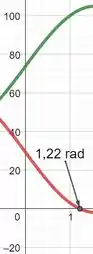
Sendo a curva verde relativa à força e a curva vermelha relativa à força .
E assim finalizamos a questão!
Resposta
