Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 47

Durante um teste de motor no solo, um empuxo é gerado sobre o avião de e com centro de massa em . As rodas principais em estão bloqueadas e não deslizam; a pequena roda sob a cauda em não tem freio. Calcule a variação percentual nas forças normais em e quando comparadas com os seus valores quando o motor do avião está desligado.

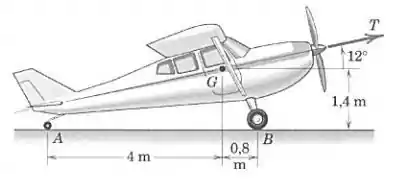
Passo 1

Quando o motor do avião está desligado, temos . Então, o equilíbrio de momentos em torno de nos dá a equação:

E o equilíbrio de forças na direção vertical nos dá:

Passo 2

Agora, na situação em que , acrescentaremos o momento dessa força na equação de momentos:

Além disso, teremos:

Passo 3

Finalmente, podemos calcular as variações percentuais e nas forças normais em e , respectivamente, quando comparadas com os seus valores quando o motor do avião está desligado:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3.36. A mola tem uma rigidez k = 800 N m e um comprimento não deformado de 200m m . Determine a força nos cabo BC e BD quando a mola é mantida na posição mostrada.

3.37. O peso de 5k g é suportado pela corda AC, pelo rolete, e por uma mola que possui uma rigidez de k = 2000 N m e um comprimento não deformado de 300 mm. Determine a distância d até onde o peso est

3.40. A mola tem uma rigidez k = 800 N m e um comprimento não deformado de 200m m . Determine a força nos cabo BC e BD quando a mola é mantida na posição mostrada.

3.41. Um cabo continuo de comprimento total 4m é passado ao redor das pequenas polias em A, B, C e D. Se cada corda está alongada em 300m m , determine a massa m de cada bloco. Despreze o peso das pol

3.26. Determine as trações desenvolvidas nos fios CD, CB e BA e o ângulo θ necessário para o equilíbrio do cilindro E de 15k g e do cilindro F de 30k g .