Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 49
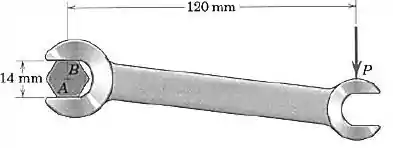
Um torque de é necessário para girar o parafuso em torno de seu eixo. Determine e as forças entre as paredes endurecidas e lisas da chave e os vértices e da cabeça hexagonal do parafuso. Considere que a chave se ajusta facilmente no parafuso, de modo que o contato é feito apenas nos vértices e .
Passo 1
O enunciado diz que precisamos de para girar o parafuso em torno do seu eixo. Como esse torque é fornecido exclusivamente pela força , que está a do centro dessa rotação:
Passo 2
Agora queremos encontrar as forças e entre as paredes da chave e os vértices do parafuso:
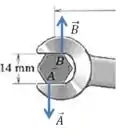
Essas forças agem sobre a chave, e não sobre o parafuso. Vamos escolher uma equação de equilíbrio de forma que o cálculo fique mais fácil:
Quando calcumamos o momento em relação ao ponto , a força vai sumir da nossa equação, então ficamos com o seguinte:
E para escrever as duas distâncias vamos precisar encontrar o comprimento de cada lado do hexágono. Sabendo que os ângulos internos medem :
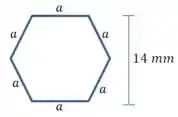
Agora podemos escrever as duas distâncias:
Então:
Passo 3
E para calcular a força podemos usar outra condição de equilíbrio:
Que é verdadeira, já que a força resultante sobre o conjunto é nula:
Resposta
As forças são , e .