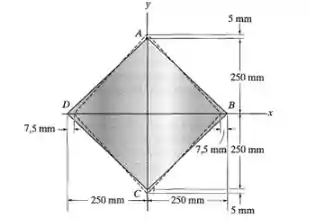
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine as deformações normais médias ao longo do lado AB e das diagonais AC e DB.
Passo 1
Falaa, meu querido! A fórmulinha da deformação normal média ao longo de um segmento de comprimento inicial é:
Precisamos então achar os comprimentos desses segmentos (final e inicial) onde ele pediu a deformação e jogar na fórmulinha, ok?
Para facilitar, a gente pode deixar aqui um esqueminha do que aconteceu:
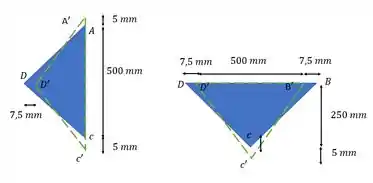
O tracejado é a situação depois da deformação. Vamos achar nossos segmentos agora!
Passo 2
Pelo esqueminha, o lado AB (que é igual a AD) originalmente valia:
Aí mudou para
Já tinha originalmente
E depois mudou para
E para o que aconteceu foi:
Passo 3
Agora, podemos calcular as deformações:
-3
-3
-3
Resposta
-3
-3
-3