Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 34
Se uma carga de 10 kg é colocada na panela, determine a posição x do bloco H de 0,75 kg para haver equilíbrio. A balança está em equilíbrio quando não há peso nem carga na balança.
Passo 1
Desenhando o diagrama do corpo livre:
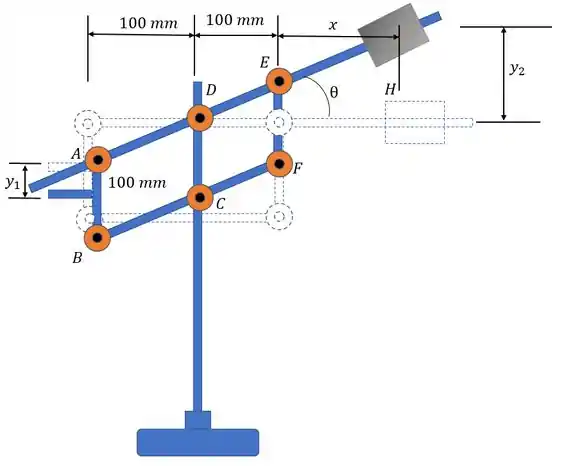
Passo 2
Da geometria do problema, temos:
Passo 3
A energia potencial do sistema é dada pela soma das energias potenciais individuais da panela e do peso na balança:
Passo 4
Para achar a posição de equilíbrio, precisamos encontrar a primeira derivada de e igualar a zero:
Resposta
Exercícios de Livros Relacionados
Se uma carga W de 450N é aplicada ao mecanismo em C, sabendo que a mola está indeformada quando θ = 15 , determine o valor de θ para equilíbrio e determine a estabilidade.
A haste AB está presa a uma articulação em A e a duas molas, cada qual de constante k. Se h = 1125 mm, k= 1kN/m e W = 270 N, determine ao menor distância d para qual o equilíbrio da haste é estável na
Duas barras AB e BC estão presas a uma única mola de constante k que está indeformada quando as barras estão na vertical. Determine o intervalo de valores de P para os quais o equilíbrio do sistema é
Duas barras estão presas a uma única mola de constante k que está indeformada quando as barras estão na vertical. Determine o intervalo de valores de P para os quais o equilíbrio do sistema é estável
A barra horizontal BEH está unida a três barras verticais. O colar em E pode se deslizar livremente sobre a barra DF. Determine o intervalo de valores de Q para os quais o equilíbrio do sistema é está