Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 54
Três forças atuam sobre o suporte. Determine a intensidade e a direção de de modo que a força resultante seja direcionada ao longo do eixo positivo e tenha uma intensidade de .
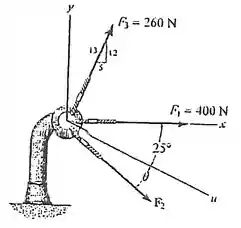
Passo 1
Fala, querido!
O exercício pede para que a gente calcule a intensidade de e o ângulo .
Repara que esse ângulo é contado do eixo . Só para facilitar nosso raciocínio, vamos achar primeiro , que vai ser o ângulo entre e o eixo , ok?
Para achar o que ele pede precisaremos decompor as forças nos eixos x e y e trabalhar com os vetores decompostos.
Ele nos dá a informação que de que a resultante é e tem direção de positivo. Repara que esse eixo tem orientação de no sentido horário em relação a x. A gente pode descobrir as componentes dessa resultante nos eixos x e y com essa informação.
Nossa força resultante está assim:
Daí a gente pode achar os valores das componentes dela nos eixos x e y:
Percebe que essa última é negativa porque a força está apontando para o sentido negativo de y.
Aí vem o pulo do gato: a gente pode achar expressões para e em função de e , calculando a componente de cada força nos eixos e somando. Comparando com esses valores aí de cima, achamos o que a questão pede!
Bora lá!
Passo 2
Vamos determinar a intensidade das forças no eixo x. Repara que para , o eixo y é oposto ao ângulo que da sua orientação. Por isso a gente coloca cosseno no x e seno no y. E repara que ela aponta para o lado positivo do eixo , aí sua componente fica positiva:
Já para , vemos que ela já está na direção de , então a componente em vai ser o próprio valor da força:
Para calcular , você tem que reparar no triângulo da figura
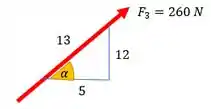
A gente vai multiplicar pelo cosseno de , já que esse ângulo tá coladinho com o eixo x. E aí vamos lembrar que
Repara que ela aponta para o sentido positivo de x.
Agora vamos calcular a intensidade da força resultante no eixo x
Passo 3
Agora a gente usa a mesma estratégia para calcular determinar as forças no eixo y
Repara que aponta para a parte negativa de y. E que o seu ângulo de orientação está colado no eixo x. Vamos usar seno aqui e deixar ela negativa:
é normal ao eixo , por isso
Vamos usar uma estratégia parecida com para calcular , mas agora usando seno, e lembrando
está no sentido positivo do eixo y, e por isso o sinal positivo
Agora vamos calcular a intensidade da força resultante no eixo y
Passo 4
Repara que agora poderemos determinar a intensidade de . Isso porque temos duas expressões para e . Podemos igualar e fazer um sisteminha!
Seguindo o mesmo raciocínio
Agora podemos elevar as duas equações ao quadrado e soma-las para sumir com e descobrir o valor de
Lembrando da relação trigonométrica , portanto:
Passo 5
Agora que sabemos a intensidade de podemos calcular o ângulo .
Aqui você pode escolher entre , eu vou usar .
Maaasss vamos precisar conferir com o :
Que é praticamente o mesmo (devem ter eerros de arredondamento).
Passo 6
Mas você pode estar se perguntando por que precisa conferir???
Se liga só na figura:
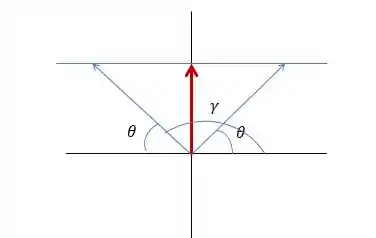
Quando a gente pega um vetor e decompõe ele no eixo y:
Ok... sem nenhum problemas.
AGOOOORA se a gente faz o contrário:
A gente ta afirmando que ele está do lado direito, massss:
E concorda que não é igual a , no caso:
A gente tem que ter uns cuidadinhos chatos, beleza?
Mas continuando a questão...
Passo 7
E lembrando que a gente quer :