Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 160

A carga de massa m recebe uma aceleração constante ascendente a pela aplicação das forças P , a partir de sua posição de repouso apoiada nos suportes. Despreze a massa das hastes em comparação com m e determine a aceleração inicial a .

Passo 1

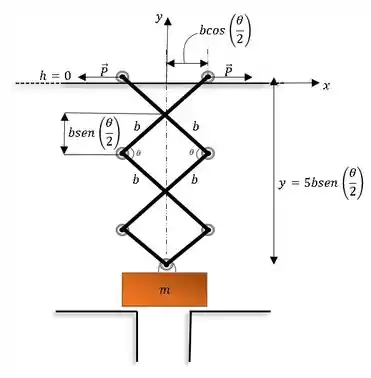
A altura y entre os roletes e a carga é dada por

y = 5 b s e n θ 2

Derivando essa expressão em relação a t , obtemos y ˙ , que é a velocidade vertical.

d y d t = y ˙ = 5 2 b θ ˙ c o s θ 2

Se derivarmos novamente com relação a t , encontramos a aceleração

d y ˙ d t = y ¨ = 5 2 b θ ¨ c o s θ 2 ⁡ - 5 4 b θ ˙ ² s e n θ 2

Para θ ˙ = 0 (condição de repouso), temos que

a =   - 5 2 b θ ¨ c o s θ 2

Passo 2

Sabemos que para um intervalo infinitesimal de movimento, a relação Trabalho-Energia é dada por

d U ' = d T + d V g

Onde

d U ' = 2 P   d x = 2 P   d b c o s θ 2 =   - P b s e n θ 2   d θ  

A variação diferencial da energia cinética é dada por

d T = d 1 2 m v ² = m v d v

Mas sabemos que v d v = a d s , sendo neste caso d s = - d y :

d T = - m a d y = - 5 2 m a b c o s θ 2 d θ  

Para a energia potencial gravitacional, temos

d V g = d m g h = d - m g 5 b s e n θ 2 = - 5 2 m g b c o s θ 2 d θ

Passo 3

Retomando a primera equação do Passo 1 e substituindo as expressões encontradas, ficamos com

- P b s e n θ 2   d θ = - 5 2 m a b c o s θ 2 d θ   - 5 2 m g b c o s θ 2 d θ

Simplificando, temos

P s e n θ 2   = 5 2 m c o s θ 2 a + g

Resolvendo para a , obtemos

a = 2 P 5 m t a n θ 2 - g

Resposta

a = 2 P 5 m t a n θ 2 - g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema mostrado na figura está em repouso quando uma força constante de 150 N é aplicada em um colar B. (a) Se a força atua por meio de todo movimento, determine a velocidade do colar B que atinge
Um bloco de 3 kg repousa sobre um bloco de 2 kg, que está preso a uma mola de constante 40 N/m. O bloco superior é subitamente removido. Determine (a) a velocidade máxima alcançada pelo bloco de 2 kg,
Os blocos A e B têm massas de 11 kg e 5 kg, respectivamente, e estão a uma altura h = 2 m acima do chão, quando o sistema é liberado do repouso. Exatamente antes de atingir o chão, o bloco A está se m
Uma corda com massa total 0,4k g e comprimento total 4m tem 0,6m de seu comprimento pendente para fora de uma bancada de trabalho. Qual será o trabalho necessário para colocar toda a corda sobre a ban
Uma criança desliza um bloco de massa 2k g ao longo de um piso de cozinha liso. Se a velocidade inicial é 4m / s e o bloco bate em uma mola com constante de mola 6N / m , qual será a conrpressão máxim