Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 22

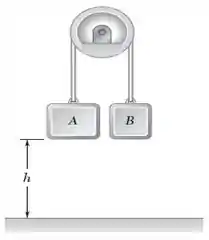
Os blocos A e B têm massas de 11 kg e 5 kg, respectivamente, e estão a uma altura h = 2 m acima do chão, quando o sistema é liberado do repouso. Exatamente antes de atingir o chão, o bloco A está se movendo com a velocidade de 3   m/s. Determine (a) a quantidade de energia dissipada no atrito das roldanas, (b) a tração em cada porção da corda durante o movimento.

Passo 1

E aí, tudo beleza? Neste problema, para o sistema mostrado na figura, temos que determinar a quantidade de energia dissipada no atrito das roldanas (item a) e a tração em cada porção da corda durante o movimento (item b), quando os blocos A e B começam a se mover.

a)

considerações:

v A = v B = v 2 = 3   m / s

v 1 = 0

T 1 = 0

T 2 = 1 2 m A + m B v 2 2

T 2 = 1 2 m A + m B v 2 2

T 2 = 16 2 3 2

T 2 = 72   J

U 1 → 2 = m A ⋅ g 2 - m B g 2 - E p

U 1 → 2 = ( 6 ) ( 9,81 ) 2 - E p

U 1 → 2 = 117,72 - E p

T 1 + U 1 → 2 = T 2

0 + 117,72 - E p = 72

E p = 117,72 - 72

E p = 45,7   J

(b)

Tração na porção da corda do bloco A:

T 1 = 0 T 2 = 1 2 m A v 2 2

T 2 = 1 2 11 3 2 = 4 9 , 5   J

U 1 → 2 = m A g - T A 2

U 1 → 2 = [ ( 11 ) ( 9,81 ) - T A ] ( 2 )

U 1 → 2 = 215,82 - 2 T A

T 1 + U 1 → 2 = T 2

0 + 215,82 - 2 T A = 49,5

T A = 83,2   N

Tração na porção da corda do bloco B:

T 1 = 0 T 2 = 1 2 m B v 2 2

T 2 = 1 2 5 3 2 = 22 , 5   J

U 1 → 2 = - m B g + T B 2

U 1 → 2 = [ - 5 9,81 + T B ] ( 2 )

U 1 → 2 = - 98,1 + 2 T B

T 1 + U 1 → 2 = T 2

0 - 98,1 + 2 T B = 22 , 5

T B = 60,3   N

Resposta

(a) 45,7   J

(b)   T A = 83,2   N ; T B = 60,3   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A esfera em A é empurrada para baixo com velocidade v 0 de intensidade 5 m/s e oscila em um plano vertical na extremidade de uma corda de comprimento l = 2m , presa a um apoio em O . Determine o ângul
A esfera em A é empurrada para baixo com velocidade v 0 e oscila em um círculo vertical de raio l e centro O . Determine a menor velocidade v 0 para que a esfera atinja o ponto B oscilando em torno do
São necessários 15 s para erguer um carro de 1200 kg e a plataforma de apoio de 300 kg de um elevador hidráulico de carros a uma altura de 2,8 m. Determine (a) a potência média de saída fornecida pela
A velocidade do elevador hidráulico do Problema 13.50 cresce uniformemente de zero até seu valor máximo a meia altura em 7,5 s e então decresce uniformemente até zero em 7,5 s. Sabendo que a maior pot
Um pequeno bloco desliza com uma velocidade v sobre uma superfície horizontal. Sabendo que h = 2,5m , determine a velocidade necessária para que ele deixe a superfície cilíndrica B C D quando θ = 40 °