Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 172
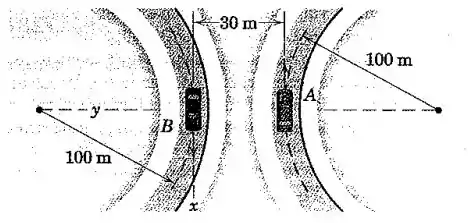
Se os carros do prob. 5/171 têm ambos uma velocidade constante de 72 km/h enquanto contornam as curvas, determine a aceleração que A parece ter para um observador se deslocando e girando com o carro B para o instante representado. Os eixos x-y estão fixados no carro B.
Passo 1
Bom galera, vamos pegar carona no exercício anterior hehe! Vejamos a Figura.
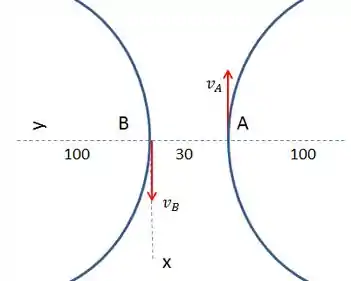
Agora, vamos buscar os dados já calculados:
Bom, vamos às acelerações. Observando individualmente as trajetórias de A e B, vemos que eles não possuem uma aceleração tangencial, apenas normal.
Vamos então relacionar os carros pela equação da aceleração relativa de eixos que giram:
Enfim, temos que:
Resposta
Exercícios de Livros Relacionados
No instante mostrado, o eixo gira com uma velocidade angular ω p = 6r a d / s e uma aceleração angular ω ˙ p = 3r a d / s 2 . No mesmo instante, o disco gira em torno de seu eixo com uma velocidade an
Resolva o problema 20.37 se a conexão em B consistir de um pino, como mostrado na figura, em vez de uma junta esférica. Dica: a restrição permite a rotação da barra tanto em torno da barra D E (direçã
O pequeno cilindro A está deslizando sobre a barra curva com velocidade u em relação à barra como mostrado. Simultaneamente, a barra está girando com velocidade angular ω em torno do ponto fixo B. Con
Se a estrada do Prob 5/168, em vez de ser reta e sem curvatura, seguir a curvatura da superfície da Terra, determine a velocidade necessária v r e l do veículo para o oeste em relação à estrada que da
Para os carros do Prob. 5/165 viajando com velocidade constante, determine a aceleração que o carro A parece ter para um observador se deslocando e girando com o carro B.