Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 157b

Para o carregamento mostrado, determinar: (b) o ponto onde a linha neutra intercepta a linha A B D . (Considere que a intensidade da força aplicada em G é aumentada de 1100   N para 1780   N .

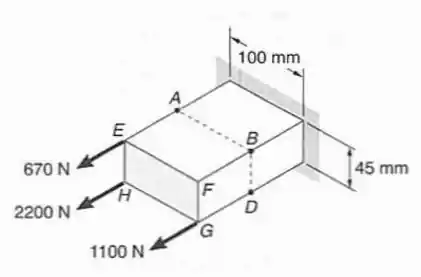
Passo 1

Para que um ponto esteja sobre a linha neutra então temos que a tensão neste ponto é igual a zero, chamando esse ponto de N temos:

σ N = P A - M z ⋅ y N I z + M y ⋅ z N I y

Como σ N = 0 (pela definição de linha neutra) temos:

0 = P A - M z ⋅ y N I z + M y ⋅ z N I y

Passo 2

Vamos olhar essa peça de uma maneira que fica mais fácila visualização. Uma vista frontal nos mostra o seguinte:

Observe que o momento M é a compisção dos momentos gerados pelas três forças atuantes na peça. Daqui a pouco iremos voltar com isso, mas antes vamos calcular os momentos de inércia:

I z = 1 12 ⋅ b ⋅ h ³

I z = 1 12 ⋅ 0,1 ⋅ 0,045 3 = 7,594 × 10 - 7   m 4

I y = 1 12 ⋅ b ⋅ h ³

I y = 1 12 ⋅ 0,045 ⋅ 0,1 3 = 3,75 × 10 - 6   m 4

Vamos calcular também a área:

A = b ⋅ h

A = 0,1 ⋅ 0,045 = 4,5 × 10 - 3   m ²

Passo 3

Agora vamos decompor o momento e a força de compressão P :

Para P não é necessário decompor porque toda ela está em x :

P = 670 + 1780 + 2200 = 4650   N

Para os momentos vamos utilizar a regra da mão direita, ou o produto vetorial (que são a mesma coisa):

M z = - 670 ⋅ 0,045 2 + 2200 ⋅ 0,045 2 + 1780 ⋅ 0,045 2

M z = 74,475   N ⋅ m

M y = + 670 ⋅ 0,1 2 + 2200 ⋅ 0,1 2 - 1780 ⋅ 0,1 2

M y = 54,5   N ⋅ m

Passo 4

Agora é só aplicar a equação:

0 = P A - M z ⋅ y N I z + M y ⋅ z N I y

Porém, perceba que não temos nenhum dos dois termos, nem z N nem y N . Mas se liga nessa sacada boladona! Se a interceptação irá ocorrer na linha A B D então ou acontece no trecho A B onde y N = 45 2 m m ou no trecho B D onde z N = - 100 / 2   m m . Vamos considerar o primeiro caso:

0 = 4650 4,5 × 10 - 3 - 74,475 ⋅ ( 0,045 / 2 ) 7,594 × 10 - 7 + 54,5 ⋅ z N 3,75 × 10 - 6

Agora vamos achar z N

0 = 1,03 - 0,22 + 14,53 ⋅ z N

z N = 0,22 - 1,03 14,53 = - 0,0557   m = - 55,7   m m

Perceba que esse valor está fora da nossa peça (UM ABSURDO)! Logo, vamos utilizar o segundo caso:

0 = 4650 4,5 × 10 - 3 - 74,475 ⋅ y N 7,594 × 10 - 7 + 54,5 ⋅ ( - 0,1 / 2 ) 3,75 × 10 - 6

0 = 1,03 - 98,1 ⋅ y N - 0,73

y N = 1,03 - 0,73 98,1 = 3   m m

Agora achamos uma resposta razoável:

z N = - 50   m m

y N = 3   m m

Resposta

z N = - 50   m m

y N = 3   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas forças P podem ser aplicadas separadamente ou ao mesmo tempo a uma placa que está soldada a uma barra circular cheia de raio r. Determine a maior tensão de compressão na barra circular.Quando amb
Sabendo que a tensão admissível na seção ABD é de 80M p a , determine a máxima intensidade da força vertical P a ser aplicada ao suporte mostrado.
Um pequeno poste de madeira suporta a carga axial de 6 kip conforme mostrado. Determine a tensão no ponto A quando: b = 0 b = 1,5i n b = 3,0i n
Podem ser aplicados até três forças axiais, cada uma da intensidade P = 50 k N , à extremidade de um perfil de aço laminado W 200 x 31,3 . Determine a tensão no ponto A.Para o carregamento mostrado,Se
Partes de 12,7 x 12,7m m de uma barra de seção quadrada foram dobradas para formar os dois componentes de maquina abaixo. Sabendo que a tensão admissível é de 103,4M p a , determine a máxima carga que