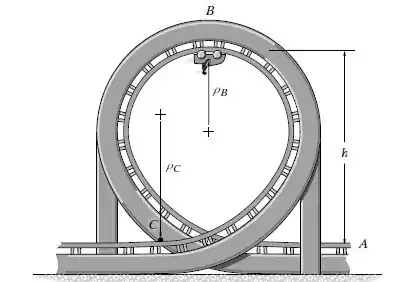
O carrinho de montanha-russa e seus passageiros têm massa total m. Determine a menor velocidade que ele tem de ter quando entra no loop A de maneira que ele possa completar a volta sem deixar os trilhos. Determine também a força normal que os trilhos exercem sobre o carrinho quando ele dá a volta e chega à parte de baixo da pista, em C. O raio de curvatura dos trilhos em B é e em C é ·. Despreze a dimensão do carrinho. Os pontos A e C estão na mesma altura.

Identificadas as energias atuantes no sistema, admitindo que sejam conservativas, a lei de conservação da energia mecânica será:

Substituindo as expressões no balanço energético, tem-se que:

Como se trata de um problema literal e de natureza curvilínea, é adequada a proposta de utilização do sistema de coordenadas normal-tangencial para auxiliar no procedimento de análise. No ponto B, tem-se a seguinte configuração:

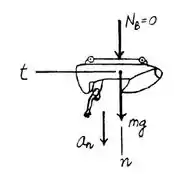
Com a condição de permanência nos trilhos e a ausência de forças na tangencial do sistema, a avaliação dinâmica é dada apenas pela componente normal. Sendo assim:

Pela lei de conservação de energia mecânica, tem-se que:

Isolando , obtém-se a seguinte expressão:

Como a avaliação da força normal do ponto C é uma incógnita, depende de diversos parâmetros que compõem o estado C, bem como a velocidade. De forma análoga aos ponto A e B, realizando a aplicação do princípio da conservação da energia mecânica para o ponto A e C.

Substituindo as expressões no balanço energético, sabendo que , tem-se que:

Por conveniência, temos que:

No ponto C, tem-se a seguinte configuração para as forças do sistema:

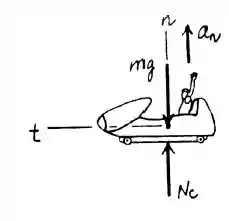
Substituindo a expressão de encontrada, tem-se que:

Colocando a massa, aceleração gravitacional e o raio de curvatura de C, a expressão final para a força normal em C será: