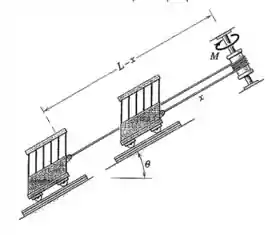
O funicular é constituído por duas cabines de passageiros, cada uma com massa , uma em cada extremidade do cabo de comprimento total e massa por uma unidade de comprimento. O sistema é operado pela aplicação de um torque ao tambor de raio no topo da via férrea. Várias voltas do cabo em torno do tambor evitam o escorregamento, e o comprimento do cabo em torno do tambor pode ser desprezado em comparação com . Se as cabines partem do repouso em com constante, desenvolva uma expressão para a velocidade de cada cabine para um determinado valor de . Despreze a massa do tambor e todo atrito.

O enunciado diz que o sistema começa com , então a energia potencial gravitacional inicial é:

Nesse caso era a altura do centro de massa do cabo mais longo quando . Vamos continuar seguindo essa mesma lógica para montar as próximas expressões.

Olhando de novo para a figura do enunciado, quando temos algum a energia potencial é:

E então:

E então a variação da energia potencial é:

Considerando que o sistema parte do repouso, a energia cinética inicial é:

E a partir daí temos:

E como todas as partes do sistema se movem com a mesma velocidade:

Então a variação da energia total do sistema é:

E nesse caso a variação da energia não é zero, porque existe um torque agindo sobre o sistema e realizando trabalho.

Então:

Agora é só resolver essa equação para encontrar a velocidade:

E então a velocidade é:

Resolvido!