A corrente inicia do repouso com um número suficiente de elos pendurados sobre a borda para apenas começar o movimento superando o atrito entre o restante da corrente e a superfície de apoio horizontal. Determine a velocidade da corrente quando o último elo passa a borda. O coeficiente de atrito dinâmico é . Despreze qualquer atrito na borda.
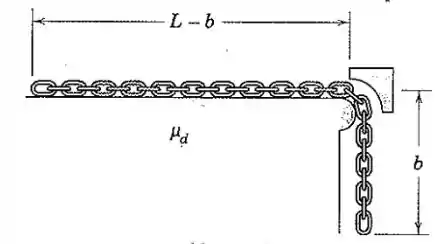
Passo 1
Vamos chamar de a densidade linear dessa corrente:
Quando uma porção de comprimento está pendurada na borda a força peso que age sobre essa porção da corrente é:
E o equilíbrio acontece se a força de atrito entre o restante da corrente e o plano é igual a :
E então:
Passo 2
Toda a energia cinética que a corrente receber terá que obedecer a essa equação:
Ou seja, terá um ganho de energia vindo da energia potencial gravitacional, e uma perda para o trabalho dissipado pela força de atrito.
A força realizada sobre um trecho da corrente é:
E então:
Passo 3
E o ganho de energia potencial gravitacional é mais fácil de calcular, será todo devido à queda da porção da corrente que começa sobre o plano.
A massa da corrente que ainda vai cair é:
E para calcular a altura devemos pensar em quanto o centro de massa da corrente desce em relação ao plano:
E então a variação de energia potencial é:
E a energia cinética é mais fácil de calcular:
Agora vamos voltar na nossa equação para a lei de conservação de energia:
E podemos resolver essa expressão para calcular a velocidade .
Passo 4
Multiplicando tudo por e dividindo pela densidade linear:
Dividindo tudo por e por :
E agora subsituímos a expressão que tínhamos encontrado para :
E agora é só simplificar:
Resolvido!
Resposta
A velocidade da corrente quando o último elo passa pela borda é .