Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 177
Calcule a velocidade máxima do cursor se o sistema é liberado a partir do repouso com . O movimento é no plano vertical. Assuma que o atrito é desprezível. Os cursores possuem massas iguais.
Passo 1
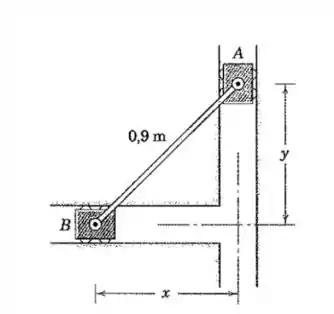
Olhando para a figura, podemos usar o teorema de pitágoras para afirmar o seguinte:
Como estamos interessados nas velocidades, vamos derivar essa equação em relação ao tempo, e pela regra da cadeia vamos ter o seguinte resultado:
Passo 2
Agora vamos aplicar a lei de conservação de energia:
A energia cinética é:
E usando a relação que descobrimos no passo :
E a energia potencial gravitacional do conjunto é:
Onde é a altura da massa (e o ângulo é de porque inicialmente temos ).
E então pela lei de conservação de energia:
E isolando a velocidade do cursor :
Mas lembrando que temos o seguinte:
Passo 3
E agora para maximizar essa função em relação ao precisamos encontrar seus pontos críticos:
E a única solução diferente de é:
Substituindo isso de volta na equação da velocidade:
Resposta
A velocidade máxima do cursor é .