Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 44
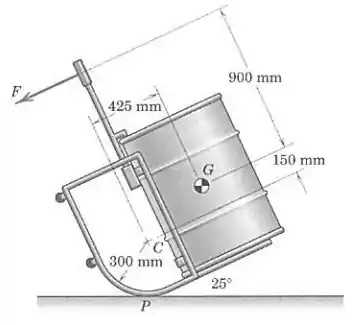
O carrinho mostrado é útil para manusear tambores grandes. Determine a força necessária para manter um tambor na posição mostrada. Você pode desprezar o peso do carrinho em comparação com o peso do tambor de , cujo centro de massa está em . Existe atrito suficiente para impedir deslizamento no ponto de contato .
Passo 1
As únicas forças que produzem momento em torno do ponto de contato são a força e o peso atuando em .
Desse modo, o equilíbrio de momentos em torno de nos dá a seguinte equação:
Resposta
Exercícios de Livros Relacionados
87. Uma mesa quadrada uniforme com peso W e lados a é sustentada por três pés verticais. Determine a menor força vertical P que pode ser aplicada em seu tampo que o fará tombar.
96. A prateleira simétrica está sujeita a uma carga uniforme de 4k P a . O apoio é fornecido por um parafuso (ou pino) localizado em cada extremidade A e A ' e por cantoneiras simétricas apoiadas cont
94. Um diagrama esquelético de perna é mostrado na figura inferior. Aqui, podemos observar que a perna é suspensa pelo músculo quadríceps conectado ao quadril em A e ao osso patela em B . Este osso de
Determine as componentes horizontal e vertical da reação em A e a reação normal em B sobre a chave no problema 5.7 .
O atuador pneumático em D é usado para aplicar uma força F = 200N no membro em B . Determine as componentes horizontal e vertical da reação no pino A e a força da barra lisa em C no membro.