Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 15
Determine as componentes horizontal e vertical da reação em e a reação normal em sobre a chave no problema .
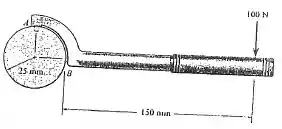
Passo 1
Então, galera, a primeira coisa que vamos analisar é a soma dos momentos em relação a !
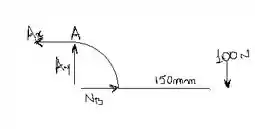
Vamos assumir que o momento no sentido anti-horário é positivo:
Passo 2
Para a gente encontrar as componentes horizontal e vertical no ponto , vamos analisar cada um dos eixos separadamente. Vamos olhar primeiro para a componente horizontal.
A soma das componentes horizontais em deve ser igual a zero na situação de equilíbrio e vamos assumir como referência a direção para direita como positiva. Assim:
Passo 3
Vamos agora para a componente vertical. A soma das componentes verticais deve ser igual a zero na situação de equilíbrio e vamos assumir como referência a direção para cima como positiva. Assim:
Resposta
Os valores para as componentes de reação em são:
O valor da reação normal em é: