Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 56
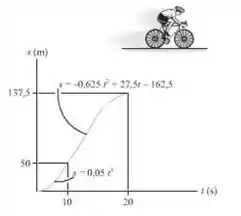
A posição de um ciclista viajando ao longo de uma estrada reta é descrita pelo gráfico. Construa os gráficos e .
Passo 1
Para a construção dos gráficos, é necessário separar os intervalos que contém diferentes equações governando o movimento do ciclista. Neste caso, temos 2 equações distintas, logo, 2 intervalos diferentes para se avaliar em cada grandeza.
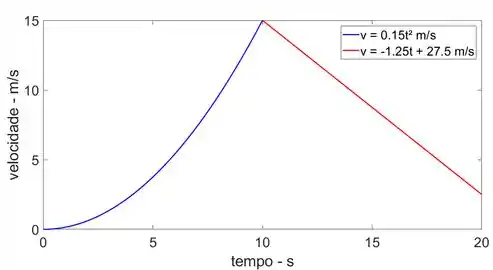
Gráfico v-t: Utilizaremos para encontrarmos a equação de velocidade.
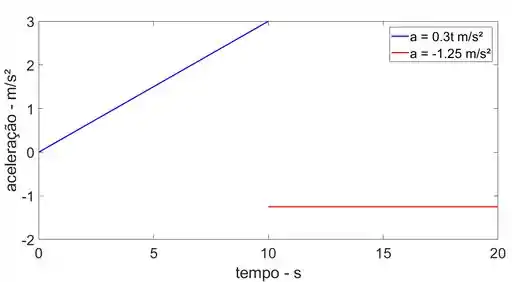
Gráfico a-t: Utilizaremos para encontrarmos a equação de aceleração.
Passo 2
Velocidade:
Para o intervalo 0
Para t = 0s e t = 10s, temos,
Para o intervalo 10
Para t = 10s e t = 20s, temos,
Aceleração:
Para o intervalo 0
Para t = 0s e t = 10s, temos,
Para o intervalo 10
Para t = 0s e t = 10s, temos,
Resposta
O gráfico está mostrado abaixo.
Exercícios de Livros Relacionados
Determine a direção da binormal à trajetória descrita pela partícula do Problema 11.96 quando (a) t = 0, (b) t = π /2 s.
Mostre que r ˙ = h ϕ ˙ sen θ sabendo que, para o instante mostrado na figura, o degrau AB do aparelho de ginástica está girando no sentido anti-horário a uma taxa constante ϕ ˙ .
Para a hélice cônica do Problema 11.95, determine o ângulo que o plano de oscilação forma com o eixo y.
O movimento de uma partícula sobre a superfície de um cilindro circular reto é definido pelas relações R = A, 2 π t e z = At2/4, onde A é uma constante. Determine as intensidades da velocidade e da ac
O movimento tridimensional de uma partícula é definido por suas coordenadas cilíndricas (veja a Fig. 11.26) R = A/(t + 1), θ = Bt e z = Ct/(t + 1). Determine as intensidades da velocidade e da acelera