Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 51
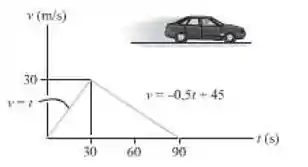
Um carro parte do repouso e move-se ao longo de uma estrada reta com uma velocidade descrita pelo gráfico. Determine a distância total percorrida até o carro parar. Construa os gráficos e .
Passo 1
Verifica-se o comportamento da velocidade ao longo do tempo e percebe-se que há 2 comportamentos distintos em diferentes intervalos de tempo. A partir destes intervalos, por meio de integração e derivação, serão indentificadas as funções que governam o deslocamento e a aceleração do carro, respectivamente.
Passo 2
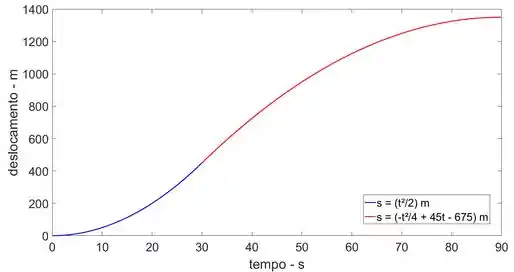
Posição:
Para o intervalo 0
Quando t = 30 s,
Para o segundo intervalo 30
Quando t = 90 s,
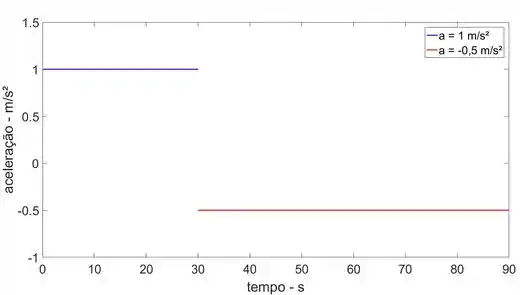
Aceleração:
Para o intervalo 0
Para o intervalo 30
Deslocamento total do carro:
Sabendo que o deslocamento total de um corpo pode ser calculado a partir da área do gráfico v-t, temos:
Resposta
Os gráficos e estão dispostos a seguir:
