Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 12
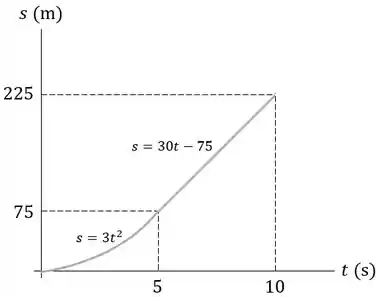
Um carro esporte move-se ao longo de uma estrada reta de tal maneira que sua posição é descrita pelo gráfico. Contrua os gráficos e para o intervalo de tempo s.
Passo 1
O enunciado nos dá dados sobre o deslocamento em função do tempo e pede para contruírmos os gráficos e para o intervalo de tempo s.
Devemos notar que, dentro deste intervalo de tempo, existem duas funções de . Portanto, devemos dividir esse intervalo de tempo em duas partes. Estas são:
Além disso, sabemos que a velocidade é igual a derivada temporal do deslocamento e que a aceleração é igual a derivada temporal da velocidade.
A partir destas informações, podemos obter os dados pedidos pela questão.
Passo 2
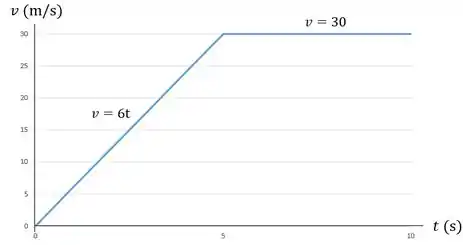
Primeiramente, vamos desenhar o gráfico .
Para isso, devemos encontrar a equação da velocidade. Sabemos que
No intervalo :
Logo, para , e para , .
No intervalo 5:
Logo, para qualquer valor de dentro deste intervalo, será constante.
O gráfico pode ser traçado da seguinte maneira:
Passo 3
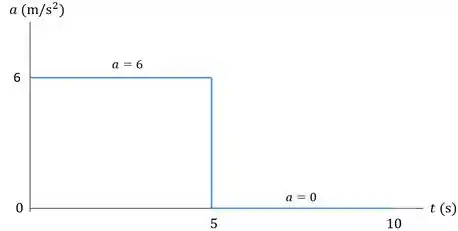
Em seguida, vamos desenhar o gráfico .
Para isso, devemos encontrar a equação da aceleração. Sabemos que
No intervalo :
Logo, para qualquer valor de neste intervalo, .
No intervalo 5:
Logo, para qualquer valor de dentro deste intervalo, será nula. O que faz sentido, pois a velocidade era constante.
O gráfico pode ser traçado da seguinte maneira:
Resposta
Ei, a resposta está no passo a passo :)