Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 64
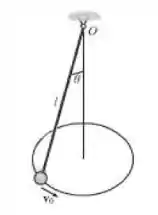
Uma bola tem massa e está ligada à corda de comprimento . A corda está amarrada no topo a uma argola móvel e é dada uma velocidade à bola. Demonstre que o ângulo que a corda faz com a vertical na medida em que a bola se move em torno da trajetória circular tem de satisfazer a equação . Despreze a resistência do ar e a dimensão da bola.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Precisamos provar uma relação. Portanto, já sabemos a resposta que devemos obter! Isto por si só já facilita bastante o problema.
Passo 2
Vamos começar por esboçar o diagrama de corpo livre do nosso problema. Desta forma, temos:
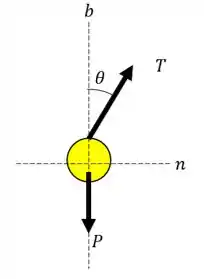
Para a nossa bola, temos apenas a ação da corça peso para baixo e a tração.
Passo 3
Vamos começar por fazer o somatório das forças na direção normal da trajetória. Desta forma, temos:
Como o raio de curvatura é , temos:
Passo 4
Agora, vamos analisar o somatório de forças na direção do eixo , perpendicular ao plano da trajetória. Nesta direção, a bola não está sujeita a acelerações. Portanto, temos:
Resposta
Ei, a resposta está no passo a passo :)