Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 27
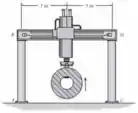
Quando o mecanismo de içamento está operando, a carga de 2000 N é submetida a uma aceleração para cima de 1,5 m/s2. Determine a força compressiva que a carga cria em cada uma das colunas, AB e CD. Qual é a força compressiva em cada uma dessas colunas se a carga está se deslocando para cima a uma velocidade constante de 0,9 m/s2? Suponha que as colunas só conseguem suportar uma carga axial.
Passo 1
Sabemos que o somatório das forças no eixo tem que ser igual a massa vezes aceleração. Então,
Para a equação do equilíbrio, temos que igualar o somatório de forças no eixo a zero. Então,
Passo 2
Pelo enunciado, , então, quando substituímos nas equações do passo 1:
E então:
Passo 3
Para a segunda pergunta do enunciado ele comenta que a velocidade é constante, isto é, aceleração será igual a zero. Então, substituindo esse valor de aceleração nas equações do Passo 1, teremos:
E então:
Resposta
– quando há aceleração de 1,5 m/s2
– quando a velocidade é constante.