Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 41

O carro, tendo uma massa de 1,40 Mg e centro de massa em G c , puxa um reboque carregado tendo uma massa de 0,8 Mg e centro de massa em G r . Determine as reações normais sobre ambas as rodas dianteiras e traseiras do carro e as rodas do reboque se o motorista aplica os freios traseiros C do carro e provoca uma derrapagem. Adote μ c = 0,4 e suponha que o engate em A é uma junta pinada ou esférica. As rodas em B e D estão livres para rodar. Despreze suas massas e a massa do motorista.

Passo 1

Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².

Para resolver esse exercício, iremos separar o sistema carro-reboque, e aplicar as equações de movimento para os dois sistemas separados conforme as figuras a seguir:

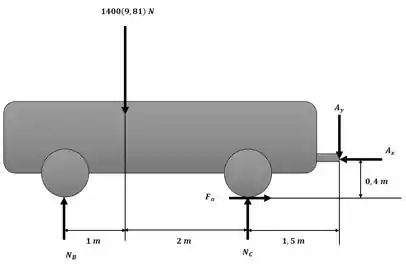
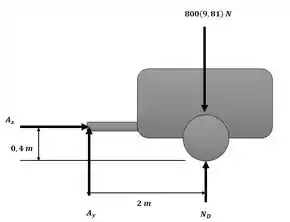
Primeiramente, aplicaremos as equações de movimento para o carro:

Sendo assim, podemos aplicar somatório de momentos em torno do ponto A:

↺ + ∑ M A = M k A

1400 9,81 3,5 + F A 0,4 - N B 4,5 - N C ( 1,5 ) = - 1400 a ( 0,35 )

1400 9,81 3,5 + 0,4 N C 0,4 - N B 4,5 - N C ( 1,5 ) = - 1400 a ( 0,35 )

Essa será nossa equação número 1.

+ ↑ ∑ F y = m a G y

N B + N C - 1400 9,81 - A y = 0

Essa será nossa equação número 2.

+ → ∑ F x = m a G x

F C - A x = 1400 a

0,4 N C - A x = 1400 a

Essa será nossa equação número 3.

Passo 2

Agora, aplicaremos as equações de movimento para o reboque:

↺ + ∑ M A = M k A

N D 2 - 800 ( 9,81 ) ( 2 ) = - 800 a ( 0,85 )

Essa será nossa equação número 4.

+ ↑ ∑ F y = m a G y

N D + A y - 800 9,81 = 0

Essa será nossa equação número 5.

+ → ∑ F x = m a G x

A x = 800 a

Essa será nossa equação número 6.

Passo 3

Agora, resolveremos o sistema de equações encontrado.

Começaremos substituindo a equação 4 na equação 5, obtemos:

N D + A y - 800 9,81 = 0

400 ( 9,81 ) ( 2 ) - 400 a ( 0,85 ) + A y - 800 9,81 = 0

A y = 340 a

Essa será nossa equação número 7.

Agora, iremos isolar o N B da equação 2 e substituir na equação 1:

1400 9,81 3,5 + 0,4 N C 0,4 - N B 4,5 - N C ( 1,5 ) = - 1400 a ( 0,35 )

1400 9,81 3,5 - ( - N C + 1400 9,81 + A y ) 4,5 - 1,34 N C = - 1400 a ( 0,35 )

48069 - ( - N C + 13734 + A y ) 4,5 - 1,34 N C = - 1400 a ( 0,35 )

Essa será nossa equação número 8.

Agora, iremos substituir o valor de A y encontrado na equação 7 na nossa equação 8:

48069 - ( - N C + 13734 + 340 a ) 4,5 - 1,34 N C = - 1400 a ( 0,35 )

Essa será nossa equação número 9.

Passo 4

Agora, iremos isolar N C da equação 3 e substituir na equação 9:

48069 - - N C + 13734 + 340 a 4,5 - 1,34 N C = - 1400 a 0,35

- 13734 + 3,16 N C = 1040 a

- 13734 + 3,16 ( A x 0,4 + 3500 a ) = 1040 a

Essa será nossa equação número 10.

Agora, iremos substituir o valor de A x encontrado na equação 6 na nossa equação 10 para obter o valor da aceleração:

- 13734 + 3,16 A x 0,4 + 3500 a = 1040 a

- 13734 + 3,16 800 a 0,4 + 3500 a = 1040 a

a = 0,8405   m / s 2

Com isso, substituindo o valor da aceleração na equação 6, obtemos:

A x = 800 a = 800 0,8405 → A x = 672,41   N

Agora, substituindo o valor de A x na equação 3, obtemos:

0,4 N C - A x = 1400 a

0,4 N C - 672,41 = 1400 0,8405 → N C = 4622,775   N

Substituindo o valor da aceleração na equação 7:

A y = 340 a = 340 0,8405 → A y = 285,77   N  

Agora, substituindo o valor de A y na equação 5:

N D + A y - 800 9,81 = 0

N D + 285,77 - 800 9,81 = 0 → N D = 7562,23   N

E, finalmente, substituindo os valores encontrados na equação 2:

N B + N C - 1400 9,81 - A y = 0

N B + 4622,775 - 1400 9,81 - 285,77 = 0

N B = 9396,99   N  

Resposta

N B = 9396,99   N  

N C = 4622,775   N

N D = 7562,23   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia da massa do pêndulo em relação a um eixo perpendicular à página e passando pelo ponto O . A barra fina tem uma massa de 10kg e a esfera tem uma massa de 15kg.
Determine o momento de inércia do conjunto de aço sólido em relação ao eixo x . O aço tem um peso específico γ = 80 KN/m3.
Determine o momento de inércia da manivela central em relação ao eixo x . O material é aço, com um peso específico γ s t = 80 KN/m3.
O dragster tem uma massa de 1200kg e um centro de massa em G . Se um paraquedas de freio é fixado em C e fornece uma força horizontal de frenagem F = 1,6 v 2N , onde v é dado em metros por segundo, de
Para o instante representado, o cursor B está se deslocando ao longo da haste fixa na direção X com uma velocidade constante v B = 4m / s . Também neste instante X = 0,3m e Y = 0,2m . Calcule a veloci