Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 39
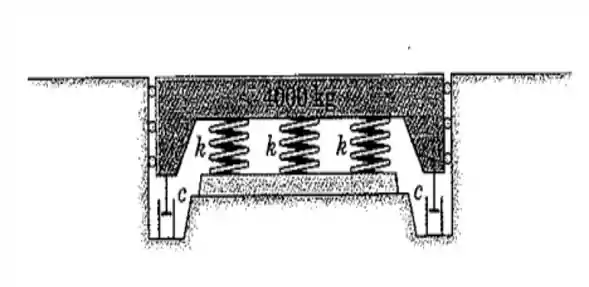
39. Um aperfeiçoamento posterior do projeto para a plataforma de pesagem do problema é apresentado aqui, onde dois amortecedores viscosos foram adicionados para limitar a razão de sucessivas amplitudes positivas de vibração vertical para , na condição descarregada. Determine o coeficiente de amortecimento viscoso necessário para cada um dos amortecedores.
Passo 1
Primeiramente, dado que temos três molas em série, cada uma com constante elástica ; o que temos que fazer é determinar a frequência angular natural do nosso sistema, que é dada pela seguinte relação abaixo:
E substituindo os valores numéricos pertencentes a cada variável, chegamos à:
Passo 2
Depois vamos atentar ao fato de que a questão nos informa que a razão entre as amplitudes sucessivas de vibração vertical, é igual a Ora bolas! Falou em “amplitudes sucessivas”, é sinônimo de decremento logarítmico , o qual tem a seguinte fórmula:
Só que:
O que já nos dá o valor do decremento logarítmico como:
Passo 3
Agora, vamos tratar de obter o fator de amortecimento , que é dado em função do descremento logarítmico como:
E substituindo o valor que encontramos para o decremento logarítmico, alcançamos nosso fator de amortecimento:
Passo 4
Pra finalizar, basta lembrar que o fator de amortecimento está relacionado com a frequência natural e o coeficiente de amortecimento viscoso pela seguinte fórmula:
E como já temos os valores que precisamos: