Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 184
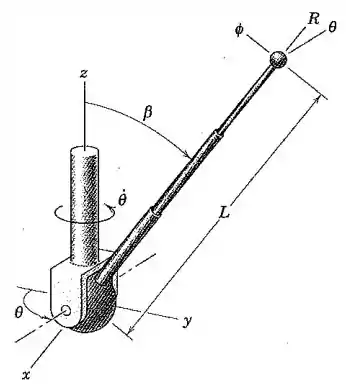
Em um teste de projeto de um mecanismo atuador para uma antena telescópica de uma espaçonave, o eixo de apoio gira em torno do eixo fixo com uma velocidade angular . Determine as componentes , e da aceleração da extremidade da antena no instante em que e se as taxas , e são constante durante o movimento.
Passo 1
Pensando em coordenadas esféricas, o enunciado nos deu os seguintes dados:
Agora vamos lembrar que as componentes da aceleração em coordenadas esféricas são dadas assim:
Passo 2
Começamos calculando :
No cálculo de , usamos a regra do produto para a derivada presente na expressão:
Passo 3
Para calcular , utilizamos novamente a regra do produto para a derivada presente na expressão:
Resposta
Exercícios de Livros Relacionados
14.26. Deduza a relação H O = r - × m v - + H G entre as quantidades de movimento angulares HO e HG definidas nas equações (14.7) e (14.24), respectivamente. Os vetores r e v definem, respectivamente,
14.28. Mostre que a Eq. (14.23) pode ser derivada diretamente da Eq. (14.11) substituindo por HO a expressão dada no Problema 14.27.
14.40 Em um jogo de bilhar, a bola A se desloca com uma velocidade v0 de intensidade v0 5 m/s quando ela atinge as bolas B e C, que se encontram em repouso e alinhadas como mostrado na figura. Sabendo
14.34. No Problema 14.5, determine a energia perdida quando o projétil (a) passa por meio do bloco A, (b) fica incrustado no bloco B.
14.41. Dois hemisférios são mantidos unidos por uma corda que mantém uma mola comprimida (a mola não está presa aos hemisférios). A energia potencial da mola comprimida é de 120 J e a montagem tem uma