O carro passa por uma depressão na estrada em A com uma velocidade constante que dá ao seu centro de massa G uma aceleração igual a 0,5 g . Se o raio de curvatura da estrada em A é de 100m , e se a distância da estrada até o centro de massa G do carro é 0,6m , determine a velocidade v do carro.

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 104

O carro passa por uma depressão na estrada em com uma velocidade constante que dá ao seu centro de massa uma aceleração igual a . Se o raio de curvatura da estrada em é de , e se a distância da estrada até o centro de massa do carro é , determine a velocidade do carro.

Passo 1

Pessoal, se o carro está com o módulo da velocidade constante em , então não há aceleração tangencial. Ou seja, toda a aceleração é a componente normal:

Mas sabemos que também se escreve assim:

onde é o módulo da velocidade e é o raio de curvatura a partir de .

Passo 2

Quando o enunciado diz que o raio de curvatura da estrada em é de , é como se existisse um círculo imaginário cuja distância do centro até o ponto fosse de . Observe a figura:

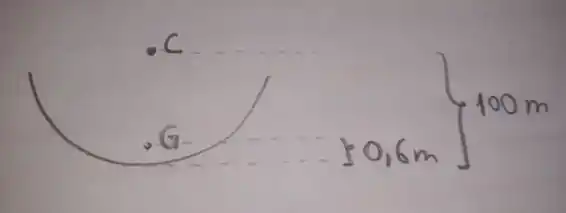
Quando analisamos o movimento do carro, as distâncias são medidas em relação ao centro de massa , então o raio de curvatura considerado para esse movimento não pode ser de . Temos que subtrair a distância de até o chão, considerando como raio de curvatura apenas a distância .

Logo, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/122) O projeto de um sistema de comando de válvulas de um motor de autonóvel de quatro cilindors é mostrado. Quando o motor é acelerado , a velocidade da correia v varia uniformemente de 3 m / s até

2/119) Um foguete viajando acima da atmosfera a uma altitude de 500k m teria uma aceleração em queda livre g = 8,43 m / s 2 na ausência de outras forças que não a atração gravitacional . Devido ao emp

2/123) Adireção do movimento de uma fita plana em um dispositivo de controle numérico é alterada pelas duas polias A e B mostradas . Se a velocidade da fita aumenta uniformemente a partir de 2 m / s a

2/125) Uma fita magnética corre sobre a polia louca em um computador conforme mostrado . Se aceleração total de um ponto P sobre a fita em contato com a polia faz um ângulo de 4 ° com a tangente á fit

2/127) Para a bola de beisebol do Prob. 2/126 , determine o raio de curvatura ρ da trajetória e a taxa de variação no tempo v ' da nos instantes t = 1s e t = 2,5s onde t = 0 é o instante do lançamento