Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 110
A roda desbalanceada possui uma masas de e rola sem deslizar sobre a superfície horizontal. Quando o centro de massa passa a linha horizontal através de como mostrado, a velocidade angular da roda é de . Calcule para esse instante e aforça normal e a força de atrito agindo sobre a roda em seu ponto de contato com a superfície horizontal. A roda possui um raio de giração em relação ao seu centro de massa de .
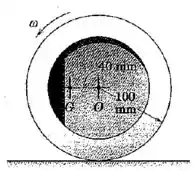
Passo 1
Vamos começar representando as forças que agem sobre a roda:
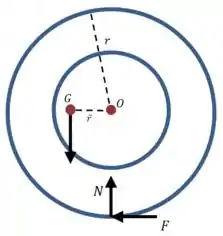
E vamos representar também as forças resultantes que agem sobre o centro de massa.
Sabemos que a roda está girando com certa aceleração angular. Isso quer dizer que temos uma aceleração centrípeta que mantém girando em torno de , uma aceleração tangencial que aumenta a velocidade angular de , e uma aceleração linear associada à translação da roda:
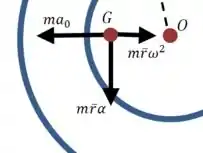
Passo 2
Agora podemos começar a montar nossas equações. Primeiro, para encontrar a aceleração , vamos considerar os momentos em relação ao ponto onde a roda faz contato com o chão:
E a única força que produz momento em torno do ponto é o peso, que está a uma distância perpendicular :
O momento de inércia pode ser calculado utilizando o raio de giração:
E para o último termo precisamos olhar para o nosso desenho das acelerações, lembrando de multiplicar cada uma por sua distância perpendicular até o ponto :
Então:
Vamos lembrar de uma relação entre e :
Agora vamos dividir tudo por e isolar :
Passo 3
Agora podemos aplicar a segunda lei de Newton nas direções horizontal e vertical para encontrar e , respectivamente:
E na direção vertical:
Resposta
As forças nesse instante são: e .