Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 105

O carro viaja com uma velocidade constante da parte inferior A da depressão para o topo B da elevação. Se o raio de curvatura da estrada em A é ρ A = 120   m e a aceleração do carro em A é 0 , 4 g , determine a velocidade v do carro. Se a aceleração em B deve ser limitada a 0,25 g , determine o raio de curvatura mínimo ρ B da estrada em B .

Passo 1

Pessoal, se o carro está com o módulo da velocidade constante, então não há aceleração tangencial. Ou seja, toda a aceleração a = 0 , 4 g é a componente normal:

a n = 0 , 4 g

Mas sabemos que a n também se escreve assim:

v 2 ρ = 0 , 4 g

v = 0 , 4 g ρ

O raio de curvatura ρ aqui tem que ser considerado a partir do centro de massa G . Observe a figura:

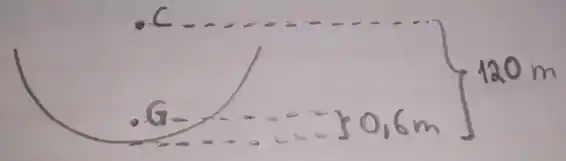
O “verdadeiro” raio de curvatura deve ser a distância C G , ou seja,

ρ = 120 - 0,6 = 119,4   m

Então, obtemos:

v = 0 , 4 9,8 119,4

v = 2 1,6   m / s

Passo 2

Se trabalharmos com o limite da aceleração, teremos em B :

a n = 0,25 g

v 2 ρ = 0,25 g

Mais uma vez, o raio de curvatura é considerado a partir de G . Observe a figura:

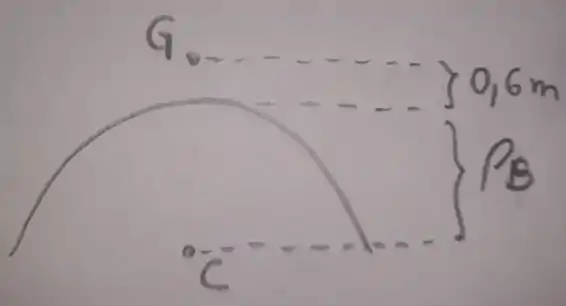
O “verdadeiro” raio de curvatura deve ser a distância C G , ou seja,

ρ = ρ B + 0,6

Então, obtemos:

v 2 ρ B + 0,6 = 0,25 g

ρ B = v 2 0,25 g - 0,6 = 21,6 2 0,25 9,8 - 0,6

ρ B = 190   m

Resposta

v = 21,6   m / s

ρ B = 190   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/132) Durante um curto intervalo as guias ranhuradas são projetadas para se deslocar de acordo com x = 16 - 12 t = 4 t 2 e y = 2 + 15 t - 3 t 2 , onde x e y são em milímetros e t é em segundos . No i
2/133) No projeto de um mecanismo de controle , a guia vertical ranhurada estase deslocando com uma velocidade constante x = 150 m m / s durante o intervalo de movimento de x = - 80 m m a x = + 80 m m
2/144) Repita o Prob.2/143 , mas agora a velocidade da partícula P está diminuindo na taxa de 20 m / s 2 enquanto se desloca ao longo da trajetória reta indicada .
2/141) O esguicho mostrado gira com uma velocidade angular Ω constante em torno de um eixo horizontal fixo através do ponto O . Devido á variação no diâmetro por um fator de 2 , a velocidade da água e
2/136) A escada de um carro de bombeiros é projetada para ser prolongada na taxa constante l ' = 6i n / s e ser elevada na taxaconstante θ = 2g r a u s / s . Quando a posição θ = 50 ° e l = 15f t é at