Determine a velocidade na qual o carro de corrida não terá tendência a deslizar lateralmente sobre a pista inclinada, isto é, a velocidade em que não existe dependência do atrito. Além disso, determine as velocidades máxima e mínima, utilizando coeficiente de atrito estático . Declare qualquer hipótese assumida.
Passo 1
A primeira pergunta é a seguinte: a qual velocidade o carro deve se mover para que ele não “precise” do atrito para se manter na curva?
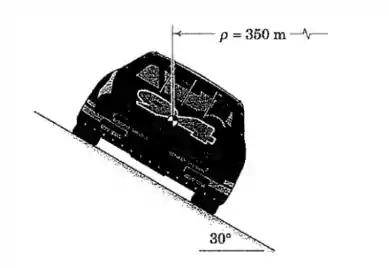
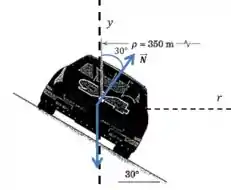
Bom, sem o atrito a única força contribuindo para a resultante centrípeta vai ser uma componente da força normal, e é ela que precisamos calcular. Vamos definir algumas direções no desenho:
Passo 2
Na direção as forças têm que estar em equilíbrio perfeito, ou seja:
Olhando para a figura, dá pra ver que essas forças são:
E as forças na direção têm que gerar uma resultante centrípeta:
Passo 3
Então ficamos com o seguinte sistema:
Pela primeira equação encontramos:
E substituindo isso na segunda:
E essa é a velocidade em que o carro não “precisa” do atrito para fazer a curva.
Passo 4
Agora queremos saber quais são as velocidades máxima e mínima em que o carro pode fazer a curva se o coeficiente de atrito estático é .
Pode parecer estranho usar o coficientede atrito estático aqui, já que o carro está se movendo. Mas é porque este coeficiente está associado ao atrito que impede que o carro deslize no sentido radial (para “dentro” ou “fora” da curva), e nesse sentido ele está de fato “parado”.
Quando a velocidade é máxima, a força centrípeta necessária para manter o movimento também é máxima, e o nosso sistema fica da seguinte forma:
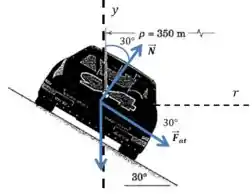
Começamos com as mesmas equações de antes:
Mas agora vamos ter um termo novo no meio:
Para resolver o sistema temos que lembrar do seguinte:
E então nossas equações ficam:
Divivindo a segunda equação pela primeira:
Passo 5
E encontrar a velocidade mínima fica tudo mais fácil: imagine que o carro está parado.
Nesse caso a força de atrito só precisa sustentar a componente do peso que é paralela ao plano:
E a força normal é igual a componente do peso que é perpendicular ao plano:
Ou seja, um coeficiente de atrito estático igual a já seria suficiente para manter o carro em equilíbrio, como podemos afirmar que o carro se mantém em equilíbrio quando .
Resposta
A velocidade em que não existe dependência do atrito é . Quando há força de atrito, as velocidades máxima e mínima são e respectivamente.