Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 220
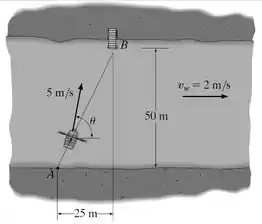
O homem consegue remar o barco na água parada com uma velocidade escalar de 5 m/s. Se o rio esta fluindo a 2 m/s, determine a velocidade escalar do barco e o ângulo que ele deve direcionar o barco de maneira que ele se desloque de A para B.
Passo 1
O homem consegue remar o barco a uma velocidade escalar de 5 m/s quando o não está fluindo, o que significa que o módulo velocidade relativa do barco em relação ao fluxo do rio será 5 m/s. O seu ângulo de direção da velocidade do barco é = 63,43°.
As velocidades da aguá, do barco e a velocidade relativa devem ser exepressas vetorialente de acordo com as suas coordenadas cartesianas, de forma que:
(1)
(2)
(3)
Passo 2
Sabendo que a equação da velocidade relativa do barco em relação a aguá é dada por :
(4)
Deve-se substituir (1), (2) e (3) em (4), de forma que:
Para a solução do problema deve-se montar um sistemas de equações de acordo com os versores i e j. De forma que :
Passo 3
Deve-se solucionar os sistemas de equações (5) e (6) de forma a se obter o módulo da velocidade do barco e seu ângulo de direcionamento .
De forma que dividindo (5) por (6) :
(7)
Ângulo é obtido pelo método de tentativa e erro aplicado a (7), de forma que :
E substituindo em (6), têm-se que :
Resposta
De acordo com os passos 1, 2 e 3 o ângulo ao qual o barco deve ser direcionado de maneira que ele se desloque de A para B será:
E a velocidade escalar do barco será: