Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 1

A velocidade de uma partícula é dada por , onde é em metros por segundo e é em segundos. Represente graficamente a velocidade e a aceleração contra o tempo para os primeiros segundos de movimento e calcule o valor de veloicdade quanto é zero.

Passo 1

Vamos começar representando a velocidade. A função em questão é a que foi dada no enunciado:

Uma boa forma de fazer isso é calcular o valor da função para cada inteiro entre e .

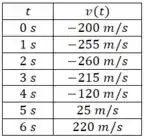
Agora você pode representar esses pontos em um gráfico e depois traçar uma trajetória mais ou menos parabólica sobre eles, já é o suficiente para um bom esboço. O resultado deve ser algo assim:

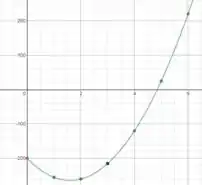
Passo 2

Agora vamos fazer uma coisa parecida para a aceleração. Para encontrar a função, só precisamos derivar a função da velocidade em relação ao tempo:

E agora fazendo a tabela:

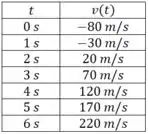
E usando o mesmo método devemos achar um gráfico parecido com esse:

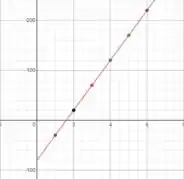
Passo 3

E agora queremos achar a velocidade quando a aceleração é igual a zero. Vamos começar descobrindo em qual instante isso acontece:

E a velocidade nesse mesmo ponto é:

Resposta

A velocidade nesse ponto é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro está viajando com uma velocidade constante v 0 = 100k m / h na parte horizontal da estrada. Quando o plano inclinado a 6 %( tan ⁡ θ = 6 / 100 ) é encontrado, o condutor não altera a posição do

Uma menina rola uma bola para cima em um plano inclinado e deixa esta retornar para ela. Para o ângulo θ e a bola em questão, a aceleração da bola ao longo da inclinação é constante em 0,25 g , dirigi

Uma força de desaceleração atua sobre uma partícula que inicialmente se desloca com uma velocidade de 100m / s e fornece uma desaceleração como a registrada pela leitura do osciloscópio mostrado na fi

Uma partícula viajando em uma linha reta encontra uma força que a retarda e provoca a redução de sua velocidade segundo v = 20 e - t / 10m / s , onde t é o tempo em segundos durante o qual a força age

Uma motocicleta parte do repouso com uma aceleração inicial de 3 m / s 2 e a aceleração então varia com a distância s como mostrado na figura. Determine a velocidade v da motocicleta quando s = 200m .