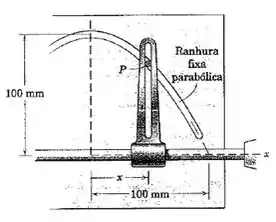
2/133) No projeto de um mecanismo de controle , a guia vertical ranhurada estase deslocando com uma velocidade constante x = 150 m m / s durante o intervalo de movimento de x = - 80 m m a x = + 80 m m . Para o instante em que x = 60m m , calcule as componente n e t da aceleração do pino P , que está confinado a se deslocar na ranhura parabólica . A partir destes resultados , determine o raio de curvatura ρ da trajetória nesta posição . Verifique seu resultado calculando ρ a partir da expressão citada no apêndice C/10 .

ρ = 19,06i n De boa galera? Então vamos para a próxima!

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 133

2/133) No projeto de um mecanismo de controle , a guia vertical ranhurada estase deslocando com uma velocidade constante durante o intervalo de movimento de a . Para o instante em que , calcule as componente e da aceleração do pino , que está confinado a se deslocar na ranhura parabólica . A partir destes resultados , determine o raio de curvatura da trajetória nesta posição . Verifique seu resultado calculando a partir da expressão citada no apêndice C/10 .

Passo 1

Então galera, a primeira coisa que devemos é organizar os nossos dados . Sabemos que :

Sendo assim, obtemos que :

Além disso , temos que :

Então ,

Logo ,

Passo 2

Bom , vamos dar uma olhada no nosso problema :

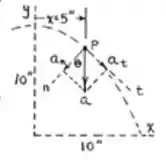
Reparem que para acharmos os valores das componentes da aceleração , precisamos primeiramente calcularmos o valor de . E para isso , utilizaremos trigonometria básica :

Agora podemos achar e através das relações :

Passo 3

Agora precisamos calcular o raio de curvatura, e paraisso precisamos achar o valor de . Sabemos que :

Para e , temos que :

Agora podemos achar o valor de através da relação :

O raio de curvatura , por sua vez , é dado por :

Checando o resultado :

Resposta

De boa galera? Então vamos para a próxima!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Partindo do repouso, o garoto core para fora na direção radial a partir do centro da plataforma com uma aceleração constante de 0,5 m/s². Se a plataforma está girando com uma velocidade constante θ ˙

A fenda do braço OA gira no sentido anti-horário em torno de O com uma velociade angular constante de θ ˙ . O movimento do pino B é restrito de tal maneira que ele se move sobre a superfície circular

Um carro move-se ao longo da curva circular de raio r = 120 m com uma velocidade escalar constante de v = 9 m/s. Determine a taxa angular de rotação θ ˙ da linha radial r e a intensidade da aceleração

Se o braço OA gira no sentido anti-horário com uma velocidade angular constante de θ ˙ = 2r a d / s , determine as intensidades da velocidade e aceleração do pino P em θ = 30 ° . O pino move-se na fen

A fenda do braço OA gira no sentido anti-horário em torno de O de tal maneira que quando θ = π / 4 , o braço OA está girando com uma velocidade angular de θ ˙ e uma aceleração angular de θ ¨ . Determi