Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 132

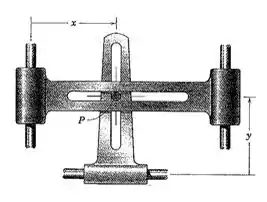
2/132) Durante um curto intervalo as guias ranhuradas são projetadas para se deslocar de acordo com e , onde e são em milímetros e é em segundos . No instante em que , determine o raio de curvatura da trajetória do pino restringido .

Passo 1

Bom pessoal , como o enunciado nos fornece a equação horária do deslocamento em relação aos eixos e , podemos achar a equação horária da velocidade e da aceleração . Temos que :

Derivando achamos a equação horária da velocidade :

Derivando mais uma vez , achamos a equação horária da aceleração :

Logo , para :

Passo 2

Para entendermos melhor o que estamos fazendo , bora dar uma olhada na representação dos valores que achamos :

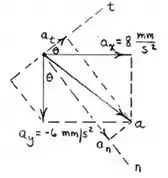
Reparem que o ângulo pode ser facilmente descoberto pelas relações trigonométricas conhecidas :

Reparem também , pela primeira imagem , que o módulo da aceleração normal pode ser obtido pela relação :

Como já conhecemos o valor da velocidade do movimento , podemos achar o raio de curvatura através da fórmula :

Resposta

Tranquilo pessoal? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro move-se ao longo de uma curva circular de raio r = 90 m. No instante mostrado, a sua taxa angular de rotação é θ ˙ = 0,4r a d / s , a qual está aumentando a uma taxa de θ ¨ = 0,2r a d / s 2 .

Uma partícula move-se ao longo de uma trajetória circular tendo um raio de 4 m, tal que sua posição como uma função do tempo é dada por θ = c o s 2 tr a d , onde t é dado em segundos. Determine a inte

Uma partícula move-se ao longo de um limaçon (ou caracol de Pascal) definido pela equação r = b - a c o s θ , onde a e b são constantes. Determine as componentes radiais e transversais da velocidade e

A posição de uma partícula é descrita por r = 300 e - 0,5 tm m e θ = 0,3 t 2r a d , onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da partícula no instante t = 1,5 s.

Uma partícula move-se ao longo de uma espiral de lituus definida pela equação r 2 θ = a 2 , onde a é uma constante. Determine as componentes radiais e transversais da velocidade e aceleração da partíc