Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 113
Um carro está viajando a descendo uma inclinação de quando os freios em todas as quatro rodas travam. Se o coeficiente de atrito dinâmico entre os pneus e a estrada é , encontre a distância medida ao longo da estrada que o carro derrapa antes de parar.
Passo 1
Perceba que o carro está subindo um plano inclinado, cuja inclinação satisfaz:
Agora, observe o seguinte diagrama de forças sobre o carro:
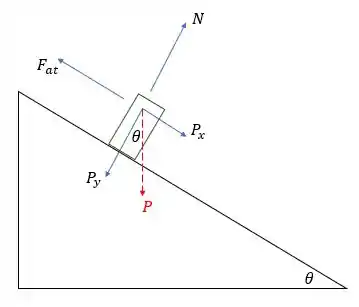
Na direção perpendicular à superfície, a componente do peso e a normal se equilibram, de modo que:
Na direção paralela à superfície, a outra componente do peso e a força de atrito atuam, de modo que a força resultante é:
Passo 2
Sabendo da força resultante na direção do movimento, calculamos o trabalho total:
Por outro lado, a variação da energia cinética será:
Passo 3
Como a variação da energia cinética de um corpo é igual ao trabalho total realizado sobre ele, temos: