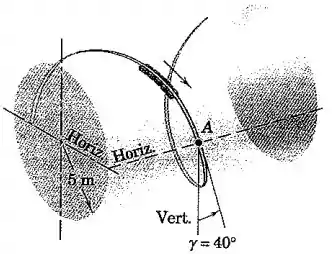
Um brinquedo de parque de diversões chamado “saca-rolha” leva os passageiros de cabeça para baixo através da curva de uma hélice cilíndrica horizontal. A velocidade dos carros quando passam pela posição é de , e a componente de sua aceleração, medida ao longo da tangente à trajetória, é neste ponto. O raio efetivo da hélice cilíndrica é de , e o ângulo da hélice é . Calcule o módulo da aceleração dos passageiros quando eles passam pela posição .

Agora, note que quando tratamos do movimento numa hélice cilíndrica, como a da figura, a mudança de direção no movimento corresponde a um movimento circular de raio , se olharmos o cilindro de frente.

Porém, essa mudança na direção é devida justamente à aceleração normal. Então, podemos escrever:

Ficamos tentados a substituir , já que essa é a velocidade do carro no ponto . Porém, lembre-se que esse movimento ocorre em três dimensões, e portanto, parte dessa velocidade não está no plano do círculo que estamos analisando. É justamente por haver uma componente de velocidade para “dentro” do cilindro, que a curva do movimento é uma hélice, e não uma circunferência.

Como o ângulo da hélice é , a velocidade no plano do círculo é:

Então a aceleração normal será:

Para calcular o módulo da aceleração, usamos a fórmula: