Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 162

2/162) O braço robótico é elevado e prolongado simultaneamente . Num determinado instante , θ = 30 ° , θ ' = 10   g r a u s s   =   c o n s t a n t e , l = 0,5   m   , l ' = 0,2 m / s e l " = - 0,3 m / s ^ 2 . Calcule os módulos da velocidade v e daaceleração a da peça P . Além disso , expresse v e a em termos dos vetores unitários i e j .

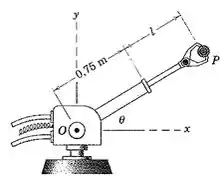
Passo 1

Bom , primeiramente bora separar as informações que já sabemos :

r = 0,75 + 0,5 = 1,25   m       θ = 30 ° r ' = 0,2 m s       θ ' = 0,1745   r a d / s r = - 0,3 m / s 2       θ = 0        

Passo 2

Agora podemos calcular as grandezas pedidas através das relações que já conhecemos :

v = v r e r + v θ e θ = r ' e r + r θ ' e θ

= 0,2 e r + 1,25 0,1745 e θ = 0,2 e r + 0,218 e θ m / s

v = v r 2 + v θ 2 = 0,296   m / s

a = a r e r + a θ e θ = ( r " - r θ ' 2 ) e r + ( 1,25 ( 0 ) ( 2 ( 0,2 ) ( 0,1745 ) ) e θ

= - 0,3 - 1,25 0,1745 2 e r + 1,25 0 + 2 0,2 0,1745 e θ

= - 0,338 e r + 0,0698 e θ m s 2

a = a r 2 + a θ 2 = 0,345 m s 2

e r = i cos ⁡ 30 ° + j sen ⁡ 30 °

e θ = - i sen ⁡ 30 ° + j cos ⁡ 30 °

v = 0,2 i cos ⁡ 30 ° + j sen ⁡ 30 ° + 0,218 ( - i sen ⁡ 30 ° + j cos ⁡ 30 ° )

= 0,064   i + 0,289   j   m / s

a =   - 0,338 i cos ⁡ 30 ° + j sen ⁡ 30 ° + 0,0698 - i sen ⁡ 30 ° + j cos ⁡ 30 °

= - 0,328   i - 0,1086   j   m / s 2

Resposta

v = 0,296   m / s

a = 0,345 m s 2

v = 0,064   i + 0,289   j   m / s

a = - 0,328   i - 0,1086   j   m / s 2

De boa pessoal? Bora continua então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/132) Durante um curto intervalo as guias ranhuradas são projetadas para se deslocar de acordo com x = 16 - 12 t = 4 t 2 e y = 2 + 15 t - 3 t 2 , onde x e y são em milímetros e t é em segundos . No i
2/133) No projeto de um mecanismo de controle , a guia vertical ranhurada estase deslocando com uma velocidade constante x = 150 m m / s durante o intervalo de movimento de x = - 80 m m a x = + 80 m m
2/144) Repita o Prob.2/143 , mas agora a velocidade da partícula P está diminuindo na taxa de 20 m / s 2 enquanto se desloca ao longo da trajetória reta indicada .
2/141) O esguicho mostrado gira com uma velocidade angular Ω constante em torno de um eixo horizontal fixo através do ponto O . Devido á variação no diâmetro por um fator de 2 , a velocidade da água e
2/136) A escada de um carro de bombeiros é projetada para ser prolongada na taxa constante l ' = 6i n / s e ser elevada na taxaconstante θ = 2g r a u s / s . Quando a posição θ = 50 ° e l = 15f t é at