Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 169

Se a estrada do Prob 5/168, em vez de ser reta e sem curvatura, seguir a curvatura da superfície da Terra, determine a velocidade necessária v r e l do veículo para o oeste em relação à estrada que dará origem à aceleração vertical nula do veículo. Assuma que o centro da Terra não possua nenhuma aceleração.

Passo 1

Bom galera, nesse exercício vamos precisar buscar o raio e a velocidade de rotação da Terra. Pela tabela D/2, temos que:

R = 6378   k m

ω = 7,292 × 10 - 5   r a d / s

Beleza! Esta questão é muito parecida com a anterior, com a diferença da trajetória circular do veículo. Vamos desenhar o sistema para entender o que isso quer dizer.

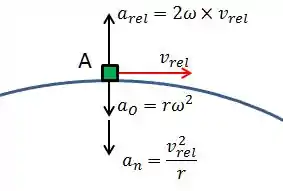
Como podemos ver na figura, surgiu outra aceleração normal a n , esta devido à trajetória circular do veículo.

Lembrando as demais acelerações: a aceleração a o que é a aceleração normal da Terra que aponta para o centro da trajetória circular; e a aceleração a r e l que é a aceleração de A em relação ao eixo que gira. Para as duas se anularem, temos que:

a O + a n = a r e l

R ω 2 + v r e l 2 R = 2 ω v r e l

v r e l 2 - 2 R ω v r e l + R ω 2 = 0

v r e l - R ω 2 = 0  

Encontramos então que:

v r e l = R ω = 6378000 ( 7,292 × 10 - 5 )

v r e l = 465,1   m / s

Resposta

v r e l = 465,1   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Próximo do final de sua corrida para decolagem, o avião está girando (arfagem do nariz para cima) imediatamente antes de levantar voo. A velocidade e a aceleração da aeronave, expressas em termos do m
A fita está sendo transferida do rolo A para o rolo B. Se o rolo B gira com uma velocidade angular constante ω O , determine uma expressão para a aceleração angular α = ω ˙ do rolo A em um instante qu
As três engrenagens 1, 2 e 3 de raios idênticos estão montadas no braço rotativo como indicado. (Os dentes de engrenagem estão omitidos no desenho). O braço AO gira no sentido horário em torno de O na
Para a posição mostrada onde θ = 30 ° , o ponto A sobre o cursor deslizante possui uma velocidade constante v = 0,3m / s com o correspondente aumento do cilindro hidráulico AC. Para essa mesma posição
No instante mostrado, o tubo gira em torno do eixo z com uma velocidade angular constante ω 1 = 2r a d / s , enquanto no mesmo instante o tubo gira para cima a uma taxa constante ω 2 = 5r a d / s . Se