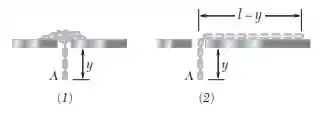
Uma corrente de comprimento e massa m cai por meio de um pequeno buraco existente em uma placa. Inicialmente, quando é muito pequeno, a corrente está em repouso. Em cada um dos casos apresentados, determine a aceleração do primeiro elo em função de , a velocidade da corrente quando o último elo dessa corrente passa por meio do furo. No caso , considere que os elos individuais permanecem em repouso até caírem por meio do buraco; no caso , considere que em qualquer instante todos os elos têm a mesma velocidade. Despreze o atrito.
Passo 1
Fala aí, galerinha. Tudo certo? Bora para mais uma questãozinha de Dinâmica:
Aplicando o limite para , temos:
Então, multiplicando os dois lados por :
Em seguida, tomando :
Agora, vamos integrar os dois lados da equação, temos:
O próximo passo é derivarmos esta equação em relação ao tempo. Vamos obter:
Passo 2
Para encontrarmos a aceleração do primeiro elo em função de no caso , temos:
E a velocidade vai ser. Utilizando a relação que encontramos no passo anterior, temos:
Passo 3
No caso , vamos aplicar a conservação de energia. Fica assim:
Logo:
Resolvendo o sistema linear entre as equações e vamos encontrar que:
E então, a aceleração vai ser:
Sabemos que:
Logo, a velocidade vai ser:
É isso, galerinha. Bora praticar mais pra ficar craque!