Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 210
O casco de aço semicilíndrico com extremidades fechadas tem uma massa de 26,6 kg. Determine a massa m do lastro de chumbo que deve ser colocado na concha de modo que ele flutue em água doce em sua profundidade de meio raio de 150 mm
Passo 1
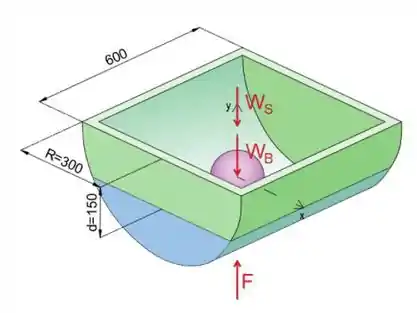
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da casca de aço com o peso da casca e a esfera de chumbo e a força de flutuação atuando nela.
O peso da carcaça de aço é:
Substitua a massa da casca e a gravidade por seus valores.
Enquanto o peso da bola de chumbo pode ser expresso como:
Passo 2
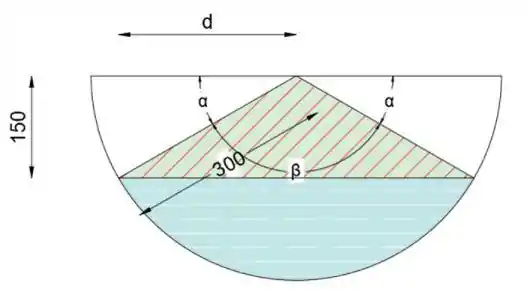
Observe que a área de um círculo cortado é igual à área do setor circular menos a área da parte triangular.
A partir do esboço, podemos ver que o ângulo α é:
E o angulo pode ser calculado:
Por fim, dimensão é:
Área do setor circular é:
Área do triângulo:
Substitua e Por seus valores na expressão (1).
Converta a área em m²
Passo 3
A força de empuxo é igual ao produto da densidade, volume e gravidade da água.
Uma vez que o comprimento é 1 = 0,6 "m, o volume da concha inundada na água é:
substitua e por seus valores e por na expressão para
Equacionando a soma das forças na direção y a zero. podemos determinar o peso total W
Substitua e por seus valores e por
A partir daqui, podemos expressar a massa do lastro como:
substitua por
Finalmente, a massa necessária para manter a casca na posição desejada é: