Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 23
23. Uma haste de peso e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto quando .
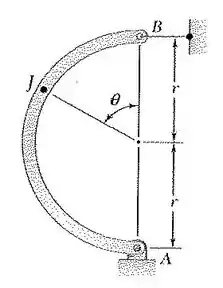
Passo 1
a) Bom! Primeiramente vamos fazer o esboço de todas as forças presentes no nosso sistema , o chamado diagrama de corpo livre:
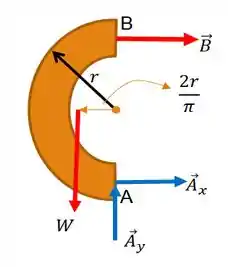
E agora, vamos tratar de fazer o somatório dos momentos em relação a um ponto de nosso interesse. Que tal o ponto ?
Depois, bora tratar de fazer o esboço de uma pequena seção do elemento ; afinal queremos achar o esforço cortante e momento fletor, para um ângulo de , não é mesmo:
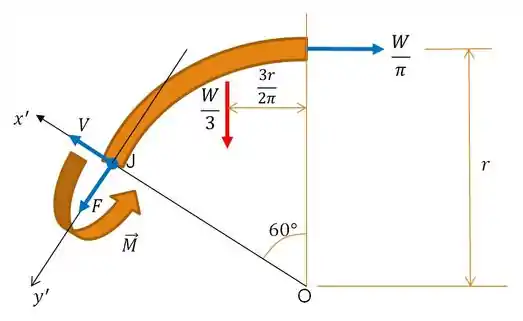
Passo 2
E agora, que definimos duas novas direções para o nosso elemento, a radial e a tangencial, vamos fazer o somatório das forças na direção tangencial, no eixo :
Dessa vez; para descobrir o quanto vale o momento fletor, vamos fazer o somatório dos momentos em relação ao ponto :
Logo, o momento fletor, que chamaremos de , é dado por: