Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 232
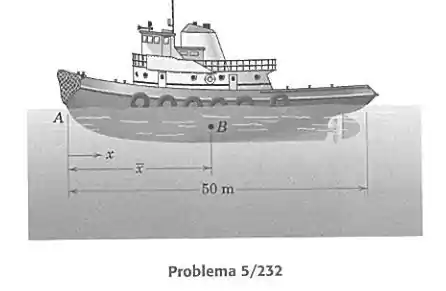
O centro de flutuação do casco de um navio é o centroide do seu volume submerso. As seções transversais das áreas submersas , ao longo da direção transversal do casco do rebocador mostrado, estão listadas na tabela para cada cinco metros de comprimento da linha d’água. Com auxílio de um programa de computador adequado, determine, com aproximação de 0,5 m, a distância de atrás do ponto .
Passo 1
O que o problema pede é a coordenada do centroide do volume submerso do navio, e então dá as áreas transversais para 11 coordenadas diferentes. Se dividirmos o corpo em 10 partes, cada uma entre duas coordenadas seguidas, cada parte terá um comprimento de 5 m, e uma área transversal que pode ser aproximada pela média aritimética da área de cada extremidade. Como exemplo, vemos na próxima figura um dos 10 volumes que compõem o volume total submerso do navio:
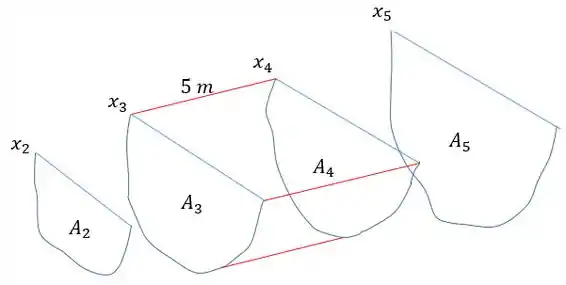
O volume do elemento entre e mostrado será então aproximado para
Passo 2
Pelo princípio dos momentos, podemos calcular a coordenada do centro de massa combinado dos 10 volumes, pela fórmula:
Já sabemos que
Com esse variando de 1 até 10. Além disso, o centro de massa de cada pequeno volume fica no meio do volume:
Então temos a nossa fórmula geral:
Passo 3
Com auxílio de um programa de computador, listamos os valores de e com indo de 1 a 10, e então fazemos os somatórios, obtendo os valores:
Então fazendo a divisão encontramos nosso valor de :