Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 74
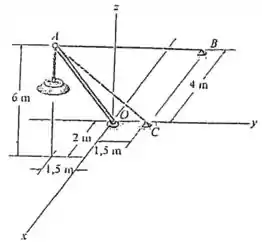
A luminária tem uma massa de 15 kg e está sustentada por uma barra AO e pelos cabos AB e AC. Se a força na barra atua ao longo de seu eixo, determine as forças em AO, AB e AC para o equilíbrio.
Passo 1
Falaaa!
Para encontrar o valor da força em cada cabo e na barra, como é pedido, o que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas.
Em seguida, o equilíbrio de forças deve ser analisado nas três dimensões x, y e z, pelo fato de as forças estarem atuando em todos esses três sentidos.
Logo, fazendo o diagrama de corpo livre tem-se:
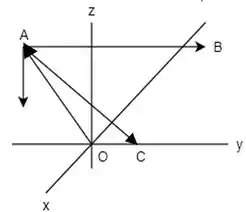
A gente escolheu esses sentidos para as forças. Mas se você escolher outro, o resultado final só vai ficar com sinal trocado.
E, então, observando o desenho feito consegue-se montar as equações de equilíbrio.
Passo 2
Tem-se que a luminária exerce uma força peso para baixo que tem intensidade de . Colocando na forma vetorial
Também é possível denotar as forças , e na forma vetorial. O que a gente precisa fazer é achar um vetor unitário na direção e sentido da força, e multiplicar a intensidade da nossa força por ele.
Percebe que para a AB, um vetor no sentido da força seria o que sai de A e vai para B. Podemos acha-lo pela diferença entre essas coordenadas desses pontos. Fazendo final menos inicial:
Aí para achar o vetor unitário só dividir esse cara pelo módulo dele. Nossa força em forma vetorial fica:
Para e fazemos algo parecido
Mas percebe que esse vetor vai de a ,mas no nosso DCL, a força está no sentido oposto, então é aí invertero sinal das coordenadas desse vetor aí e continuar as contas
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Olhando para cada eixo, vamos igualar a soma em cada componente a zero:
Para as componentes em , por fim,
Passo 4
Agora, como há três equações encontradas, é possível montar um sistema de equações linear e determinar a solução dele, cuja solução será o valor das forças.
Resolvendo este sistema, obtem-se: