Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 136
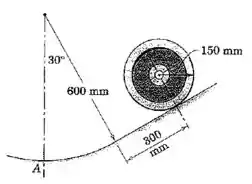
O centro da roda de com raio de giração centroidal de tem uma velocidade de para baixo na inclinação na posição indicada. Calcule a reação normal sob a roda quando ela passa pela posição . Assuma que não há deslizamento.
Passo 1
Quando a roda passa pelo ponto , deve haver uma resultante centrípeta apontando para cima:
Então, para encontrar a força normal, nós precisamos determinar a velocidade do centro de massa da roda quando ela chega no ponto .
Passo 2
Para encontrar essa velocidade , vamos usar a lei de conservação de energia:
Começamos encontrando uma expressão para a variação de energia potencial gravitacional:
O plano é inclinado por , então ao percorrer a distância de ao longo do plano, todas os pontos da esfera terão descido pela seguinte altura:
Em seguida, o centro de massa fará um movimento análogo ao de um pêndulo, com um raio de curvatura , de forma que o seu deslocamento vertical ao completar um arco de será:
Então:
Então:
Passo 3
Agora vamos encontrar uma expressão para a variação de energia cinética:
Perceba que, se é o ponto de contato entre a superfície e a roda, nós só precisamos considerar a energia cinética de rotação, pois a velocidade linear de é sempre nula.
E fica faltando calcular o momento de inércia em relação ao ponto , usando o teorema dos eixos paralelos:
Então:
Passo 4
Agora vamos retomar a nossa lei de conservação de energia:
E agora é só substituir na expressão que escrevemos no primeiro passo:
Resposta
A reação normal sobre a roda é no ponto mais baixo da trajetória.