Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 101
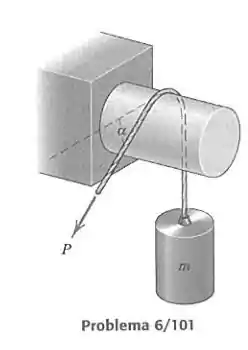
Para um certo coeficiente de atrito e um certo ângulo , a força necessária para elevar vale 4 kN e a necessária para abaixar vale 1,6 kN. Calcule a massa .
Passo 1
No limiar de escorregamento da corda, tanto para um lado quanto para o outro, ela está em equilíbrio, dado pela fórmula:
Sendo e as trações maior e menor nas extremidades da corda, o coeficiente de atrito entre a corda e a superfície e o ângulo total de giro da corda. Para levantar a massa, a tração maior é 4 kN e a menor é o peso de . Para abaixar, a tração maior é feita pelo peso , e a menor é de 1,6 kN. Aplicando então as duas equações devemos achar .
Passo 2
Então aplicamos a primeira equação, para o levantamento da massa , sendo a aceleração da gravidade:
Agora aplicamos a segunda, para abaixar a massa. Dessa vez e :
Das duas equações tiramos:
Aplicando a raiz quadrada chegamos ao valor de :