Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 08

O cilindro de 50 kg tem uma velocidade angular de 30 rad/s quando é colocado em contato com a superfície horizontal em C. Se o coeficiente de atrito cinético é μ C = 0,2 , determine quanto tempo vai levar para o cilindro parar de girar. Que força é desenvolvida no membro AB durante esse tempo? O eixo através do cilindro está conectado a dois membros simétricos (apenas AB é mostrado). Para o cálculo, despreze o peso dos membros.

Passo 1

Resolveremos esse exercício adotando a aceleração da gravidade g =   9,81   m / s 2 .

Para resolver esse problema, devemos aplicar o princípio do impulso e momento nas direções x e y e também o princípio do impulso e momento angular. Antes, calculemos o momento de inércia ao redor do centro de massa:

I G = 1 2 50 0,2 2 → I G = 1   k g . m 2

Passo 2

Sendo assim, com o auxílio do esquema a seguir:

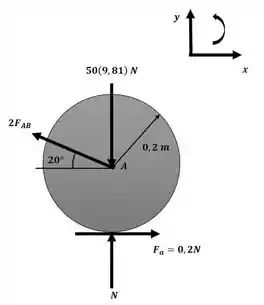
Aplicando o princípio do impulso e momento na direção x:

+ →   m v G x 1 + ∑ ∫ t 1 t 2 F x d t = m v G x 2

0 + 0,2 N t - 2 F A B c o s 20 ° t = 0

F A B = 0,10641 N

Essa será nossa equação número 1. Agora, aplicando na direção y:

+ ↑   m v G y 1 + ∑ ∫ t 1 t 2 F y d t = m v G y 2

  0 + N t + 2 F A B s e n 20 ° t - 50 9,81 t = 0

Essa será nossa equação número 2. Agora o princípio do impulso e momento angular:

↺ +   I G ω 1 + ∑ ∫ t 1 t 2 M G d t = I G ω 2

- 1 30 + 0,2 N t 0,2 = 0

t = 750 N

Passo 3

Agora devemos resolver o sistema de equações encontrado no passo 2. Começaremos substituindo a equação 3 na equação 2:

  0 + N t + 2 F A B s e n 20 ° t - 50 9,81 t = 0

0 + N 750 N + 2 F A B s e n 20 ° 750 N - 490,5 750 N = 0

F A B = 717,06 - 1,4619 N

Agora, substituiremos esse valor na equação 1:

F A B = 0,10641 N

717,06 - 1,4619 N = 0,10641 N

N = 457,22   N

Agora, podemos substituir esse valor na equação 1:

F A B = 0,10641 N

F A B = 0,10641 457,22 → F A B = 48,65   N

E, por fim, substiruiremos o valor de N na equação 3:

t = 750 N

t = 750 457,22 → t = 1,64   s

Resposta

t = 1,64   s

F A B = 48,65   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No conjunto giratório mostrado, o braço O A e a carcaça vinculada do motor B têm uma massa combinada de 4,5k g e um raio de giração em relação ao eixo z de 175m m . A armadura do motor e o disco conec
A esfera homogênea de massa m e raio r é projetada ao longo da inclinação de ângulo θ com uma velocidade inicial v o e sem velocidade angular ( ω o = 0 ) . Se o coeficiente de atrito dinâmico é μ k ,
As três barras estão livres para girar em torno do eixo horizontal fixo x em O . Cada uma das barras A tem uma massa de 20k g , um raio de giração em relação ao eixo x de 300m m , e um centro de massa
A barra esbelta uniforme de massa m e comprimento l tem velocidade angular nula quando a extremidade A bate no chão sem nenhum movimento de retorno. Para um determinado valor da velocidade v 1 pouco a
Uma pessoa que passa através da porta giratória exerce uma força horizontal de 90 N em um dos quatro painéis da porta. Se cada painel e modelado por uma placa retangular uniforme de 60 kg com 1,2 m de