Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 195

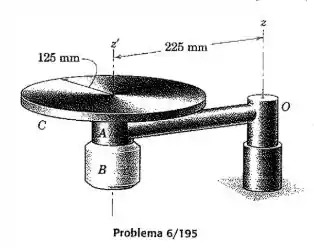
No conjunto giratório mostrado, o braço O A e a carcaça vinculada do motor B têm uma massa combinada de 4,5   k g e um raio de giração em relação ao eixo z de 175   m m . A armadura do motor e o disco conectado de 125   m m de raio têm uma massa combinada de 7   k g e um raio de giração de 100   m m em relação ao seu próprio eixo. O conjunto todo é livre para girar em relação ao eixo z . Se o motor é ligado com O A inicialmente em repouso, determine a velocidade angular N de O A , quando o motor tiver atingido uma velocidade de 300   r p m relativa ao braço O A .

Passo 1

Este problem merece atenção especial pois utiliza o conceito de velocidade relativa. A questão pede a velocidade angular N de O A quando o motor tiver atingidio uma velocidade de ω r e l = 300   r p m relativa ao braço O A .

Assim, seja ω o a velocidade absoluta do conjunto armadura do motor e disco. Então, temos

ω o = ω r e l - N

Caso isto não esteja 100% claro, você pode procurar a aula que temos sobre velocidade relativa pra ficar craque no assunto!

Passo 2

Pela conservação da quantidade de movimento angular, temos

H o 1 = H o 2 = 0

Para a armadura do motor e o disco, temos

H o = I o ω = 4,5 0,175 2 N = 0,138 N

Já para o braço O A

H o = I o ' ω o - m r N = 7 0,1 2 ω r e l - N - 7 0,225 2 N

Mas, pelo enunciado, sabemos que

ω r e l = 300   r p m = 300 × 2 π 60 = 31,4   r a d / s

Substituindo ω r e l na equação anterior:

H o = 0,07 31,4 - N - 0,354 N = - 0,424 N + 2,198

Passo 3

Igualando as quantidades de movimento angular, temos

0,138 N = - 0,424 N + 2,198

Por fim, resolvendo para N , obtemos

N = 3,88   r a d / s = 3,88 × 60 2 π   r p m = 37,0   r p m

Resposta

N = 37,0   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motor de 400 kg apoiado por quatro molas, cada uma com 150 kN / m constantes, é obrigado a se mover verticalmente. Sabendo que o desequilíbrio do rotor é equivalente a uma massa de 23 g localizada
Uma placa quadrada fina do lado a pode oscilar em torno de um eixo AB localizado a uma distância b de seu centro de massa G. (a) Determine o período de pequenas oscilações se if b = 1 2 a ⋅ ( b ) Dete
Duas hastes, cada uma com massa m e comprimento L, são soldadas para formar o conjunto mostrado. Determine (a) a distância b para a qual a frequência de pequenas oscilações da montagem é máxima, (b) a
19.114. À medida que a velocidade de rotação de um motor de 100 kg apoiado por molas é aumentada, a amplitude da vibração, causada pelo desbalanceamento do seu rotor de 15 kg, primeiro aumenta e depoi
19.117. Um motor de 100 kg é parafusado a uma viga horizontal leve. O desbalanceamento do seu rotor é equivalente a uma massa de 60 g localizada a 100 mm do eixo de rotação. Sabendo que a ressonância